Contrib:KeesWouters/shell/static
Contents
Static analysis of a shell construction
This contribution is in close cooperation with Bridge.
In this example the following items are discussed:
- preproccesing:
- definition of geometry in Salome
- partitioning of the geometry and groups
- meshing of the geometry
- definition of the groups
- (maybe: python script which makes editing much easier ...)
- static analysis with pressure or force applied on a group or nodes
- postprocessing:
- viewing displacement in Salome
- determination of stresses, see also tables
- interface ASTK
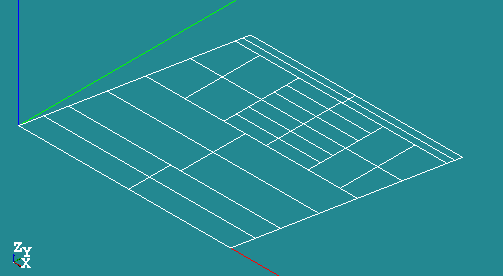
Definition of the geometry
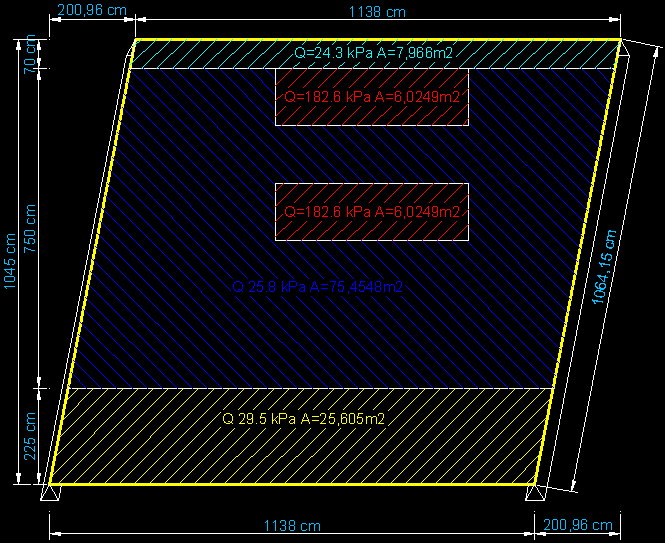
planar shell
Geometry:
- L = 11.38 m
- Thickness = 0.55 m
Loads:
[type] [group] [value]
- Presure1 (Fbot) = 29.5e3 Pa
- Presure2 (Fmain)= 25.8e3 Pa
- Presure3 (Ftop) = 24.3e3 Pa
- Presure4 (Fcentre1,Fcentre2)= 182.6e3 Pa
Boundary conditions:
- Lbot (DX=0.0, DY=0.0, DZ=0.0)
- Ltop (DZ=0.0)
Material:
Concrete
- E = 32e9 Pa
- Nu = 0.2
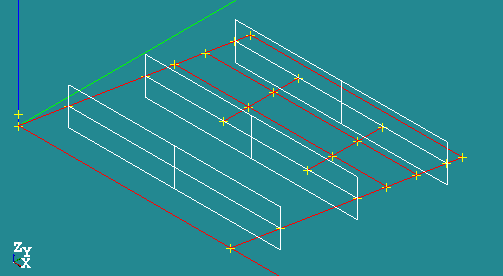
Create all points and lines using: [New Entity]->[Basic}->[Point] and [New Entity]->[Basic]->[Line]
 :
: 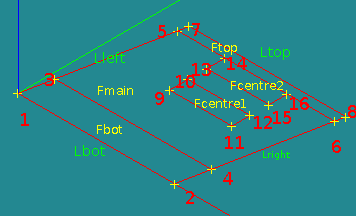
In the command file the edges and faces are named as shown in the right figure.
The coordinates are:
P1 = geompy.MakeVertex( 0.000, 0.00, 0.00) P2 = geompy.MakeVertex( 11.380, 0.00, 0.00) P3 = geompy.MakeVertex( 0.433, 2.25, 0.00) P4 = geompy.MakeVertex( 11.813, 2.25, 0.00) P5 = geompy.MakeVertex( 1.875, 9.75, 0.00) P6 = geompy.MakeVertex( 13.255, 9.75, 0.00) P7 = geompy.MakeVertex( 2.010, 10.45, 0.00) P8 = geompy.MakeVertex( 13.390, 10.45, 0.00)
P9 = geompy.MakeVertex( 5.300, 5.72, 0.00) P10 = geompy.MakeVertex( 5.300, 7.05, 0.00) P11 = geompy.MakeVertex( 9.830, 5.72, 0.00) P12 = geompy.MakeVertex( 9.830, 7.05, 0.00) P13 = geompy.MakeVertex( 5.300, 8.42, 0.00) P14 = geompy.MakeVertex( 5.300, 9.75, 0.00) P15 = geompy.MakeVertex( 9.830, 8.42, 0.00) P16 = geompy.MakeVertex( 9.830, 9.75, 0.00)
Create one big face Ftotal [New Entity]->[Build]->[Face]
Ftotal: Line7,Line6,Line8,Line12,Line11,Line10,Line9,Line1

Create three wires [New Entity]->[Build]->[Wire]
- Wire1: Line3,Line4,Line5
- Wire2: Line17,Line18,Line19
- Wire3: Line13,Line14,Line15,Line16
Create vector [New Entity]->[Basic]->[Vector]
(0,0,1)
Create four extrusions [New Entity]->[Generation]->[Extrusion]
- Extrusion1: Wire1,vz
- Extrusion2: Wire2,vz
- Extrusion3: Wire3,vz
- Extrusion4: Line2,vz
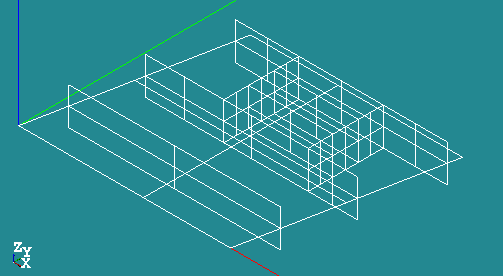
Partitioning of the geometry
Why do we need to partition the geometry? We need geometrical entities or groups for loads and boundary conditions. Partitioning the geometry makes sure that the for resulting mesh each group is meshed along its borders correctly and the mesh is connected between these groups.
Partitioning process: the geometry is divided by planes or other 2D surfaces. These Tool objects need to divide the geometry completely in two seperate parts. In Salome several Tool objects can be chosen in one Partition operation. After the partitioning the groups need to be created. In the Aster command file these groups can be used to define loads, boundary conditions, displacements, stresses, strains etc.
Create partition [Operations]->[Partition]
- Part_main: Ftotal,Extrusion1,Extrusion2,Extrusion3,Extrusion4
Create two groups for boundary conditions [New Entity]->[Group]->[Create]
Shape type: line
Main Shape: Part_main
- Lleft: left lines: Line7,Line8,Line9
- Lright: right lines: Line10,Line11,Line12
Triangle mesh
Set Mesh 1D: Composite Side discretisation
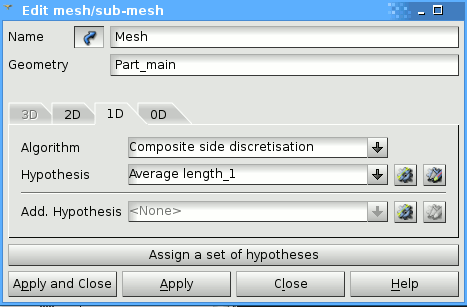
Set Mesh 1D Average lenght: 0,5

Mesh 2D settings: Netgen 2d
Mesh info:
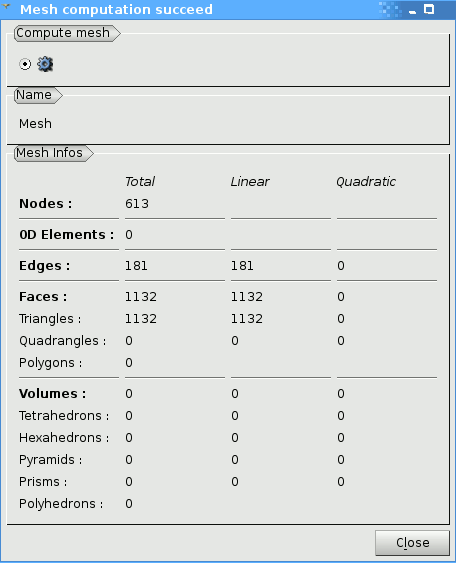
Computed Mesh:

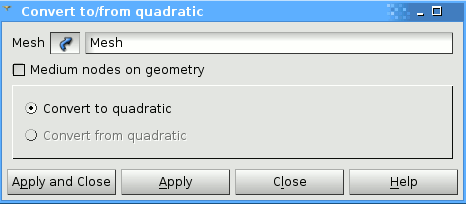
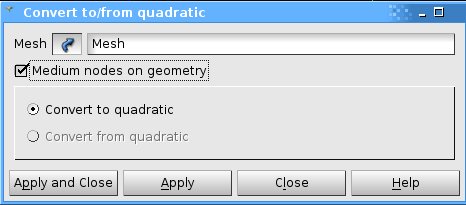
Since we are going to use COQUE_3D elements in the calculation, we need quadratic elements. So we convert the linear to quadratic mesh. If you want to make sure that the midside nodes will be locked to the geometry, you can tick the medium nodes on geometry.
Save the mesh: in the mesh module, right click on the <mesh_name> --> Export to MED file, give file name or accept default (Mesh.med in this case) and <save>. Now the mesh is available for Aster and calculations can be performed.
Hexa mesh
This geometry is not good enough for hexa mesh.
For hexa mesh we need little bit more complicated geometry.
- points and lines
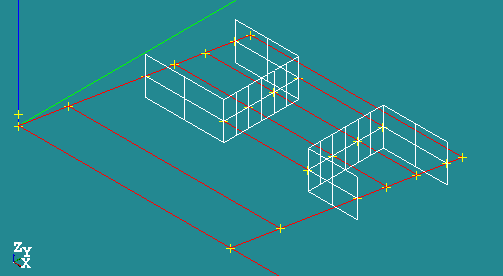
Create six wires [New Entity]->[Build]->[Wire]
- wire 1, wire 2, wire 3
- wire 4, wire 5
- wire 6
Create vector [New Entity]->[Basic]->[Vector]
(0,0,1)
Create four extrusions [New Entity]->[Generation]->[Extrusion]
- Extrusion1: Wire1,vz
- Extrusion2: Wire2,vz
- Extrusion3: Wire3,vz
- Extrusion4: Wire4,vz
- Extrusion5: Wire5,vz
- Extrusion6: Wire6,vz
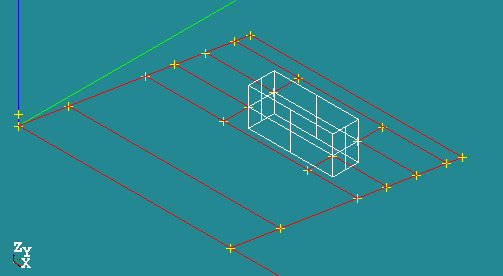
Create one big face Ftotal [New Entity]->[Build]->[Face]
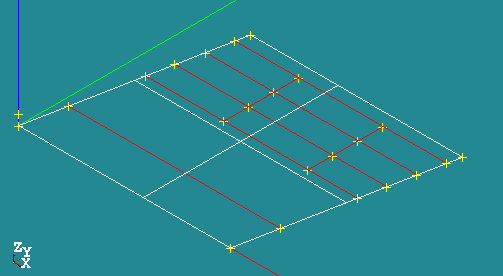
Create partition [Operations]->[Partition]
- Part_main: Ftotal,Extrusion1,Extrusion2,Extrusion3,Extrusion4,Extrusion5,Extrusion6 (all extruded wires)
- Part_main
Create three groups for loads [New Entity]->[Group]->[Create]
Shape type: face
Main Shape: Part_main
- groups: ftop, fbot
- groups: fmain
- groups: fcentre1, fcentre2
Create two groups for boundary conditions [New Entity]->[Group]->[Create]
Shape type: line
Main Shape: Part_main
- Lleft: left lines
- Lright: right lines
- Create hexa mesh: Assign a Set of Hypotheses Automatic Hexahedralization

Set Mesh 1D: Composite Side discretisation
Set Mesh 1D Average lenght: 0,5

Mesh 2D settings: Quadrangle
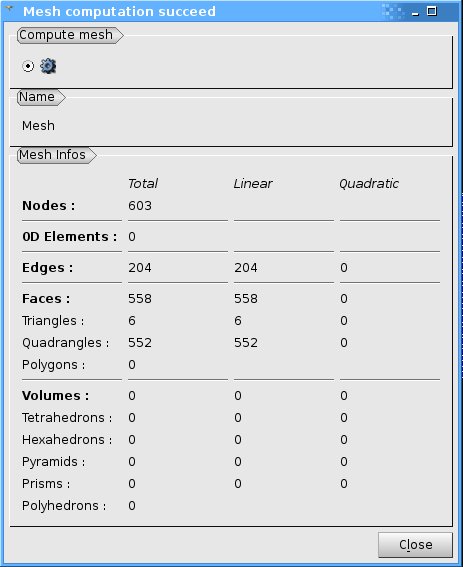
Computed Mesh:

Mesh info:
Convert to quad mesh
ASTK - Aster
General way of working
For the calculations we need two input files:
- mesh file, this has been discussed in the previous part
- command file, a list of commands for processing by Aster
Several output files are generated by Aster, look here for more [information]. ASTK is the interface for defining input and output files that are needed by Aster. The mesh file is already available so we are going to discuss the command file now.
The comm files is sequence of commands processed by Aster. In this case the rough outline is:
- read the mesh file
- define material and mechanical properties to the geometrical entities
- define a model
- perform the calculations
- determine the displacements and stresses at the nodes based on the previous step
- write the quantities to a result mesh file
Detailed commands
Reading mesh and applying the model
Here the commands are discussed in detail.
In principle these are a Python commands. Any valid Python expression can be inserted in the command file.
First command is always DEBUT. The initial mesh meshinit is read. This is now a quadratic triangular mesh. Each triangle has 6 nodes: 3 corner nodes and 3 midside nodes. Since we are going to use a COQUE_3D modelisation, that uses 7 nodes for a triangle, we need to convert this mesh to meshmod.
- meshmod <-- meshinit [CREA_MAILLAGE]
To control the orientation of the normals of meshmod we use MODI_MAILLAGE to make sure that normals of all triangles point in the same direction and we can give these normals a dedicated direction.
Based on the meshes mechanical models are built:
- modeinit <-- meshinit <-- 6 nodes triangle [AFFE_MODELE]
- modmod <-- meshmod <-- 7 nodes triangle [AFFE_MODELE]
definition of models
DEBUT();
meshinit=LIRE_MAILLAGE(FORMAT='MED',);
modinit=AFFE_MODELE(MAILLAGE=meshinit,
AFFE=_F(GROUP_MA= ('Fbot','Fmain','Ftop','Fcentre1','Fcentre2',),
PHENOMENE='MECANIQUE',
MODELISATION='3D',),);
meshmod=CREA_MAILLAGE(MAILLAGE=meshinit,
MODI_MAILLE=_F(TOUT='OUI',OPTION='TRIA6_7',),);
meshmod=MODI_MAILLAGE(reuse =meshmod,
MAILLAGE=meshmod,
ORIE_NORM_COQUE=_F(GROUP_MA=('Fbot','Fmain','Ftop','Fcentre1','Fcentre2',),),);
###VECT_NORM= (0,0,+1),NOEUD='N19'),);
modmod=AFFE_MODELE(MAILLAGE=meshmod,
AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',
MODELISATION='COQUE_3D',),);
shell - mechanical properties
The shell characteristics are not defined in the mesh. So parameters like thickness need to determined here. All the shell characteristics are defined by the AFFE_CARA_ELEM command:
- the model to be used MODELE
- the geometrical parts on which it applies: COQUE=_F(parts)
- thickness EPAIS
- number of layers COQUE_NCOU (one is enough for a linear calculation)
- local coordinate system by VECTEUR=(lx,ly,lz). The projection of this vector on the shell defines the local x axis. The local y axis is perpendicular to the local x axis in the shell plane. The local z axis is -hence- the normal on the plane. Default value is global x axis (1,0,0). This is important for local stresses (SIXX, SIYY, SIZZ, SIXY, SIXZ and SIYZ) and strains.
- offset EXCENTREMENT (not applicable for COQUE_3D modelisation).
th = 0.55
shellch=AFFE_CARA_ELEM(MODELE=modmod,
COQUE=_F(GROUP_MA=('Fbot','Fmain','Ftop','Fcentre1','Fcentre2',),
EPAIS=th,
VECTEUR=(1.0,0.0,0.0,),
COQUE_NCOU=1,
EXCENTREMENT=0.000),);
You can define the material properties by DEFI_MATERIAU
steel=DEFI_MATERIAU(ELAS=_F(E=210000000000.0,
NU=0.3,
RHO=7850.0,),);
concrete=DEFI_MATERIAU(ELAS=_F(E=32000000000.0,
NU=0.2,
RHO=2500.0,),);
The material properties need to applied to the selected parts of the geometry, in this case all parts are selected (TOUT='OUI')
material=AFFE_MATERIAU(MAILLAGE=meshmod,
AFFE=_F(TOUT='OUI',
MATER=concrete,),);
Applying load and boundary conditions on the construction by the command AFFE_CHAR_MECA. The key words are:
- loads are applied to model: MODELE=modmod
- defintion of prescribed displacements by DDL_IMPO applied on several groups
- ... geometrical group: GROUP_MA=(part),
- ... fixed displacement in directions eg DX=DY=DZ=0.00
- apply a pressure on groups: FORCE_COQUE
- ... geometrical group: GROUP_MA=(part),
- ... value of pressue PRES=pressure
load_bc=AFFE_CHAR_MECA(MODELE=modmod,
DDL_IMPO=(_F(GROUP_MA='Lleft',
DX=0.0,
DY=0.0,
DZ=0.0,),
_F(GROUP_MA='Lright',
DZ=0.0,),),
FORCE_COQUE=(_F(GROUP_MA='Fbot',
PRES=29.5e3,),
_F(GROUP_MA='Fmain',
PRES=25.8e3,),
_F(GROUP_MA='Ftop',
PRES=24.3e3,),
_F(GROUP_MA=('Fcentre1','Fcentre2',),
PRES=182.6e3,),),);
static calculation
resu=MECA_STATIQUE(MODELE=modmod,
CHAM_MATER=material,
CARA_ELEM=shellch,
EXCIT=_F(CHARGE=load_bc,),
OPTION='SIEF_ELGA_DEPL',);
determine element and nodel properties
resu=CALC_ELEM(reuse =resu,
MODELE=modmod,
CHAM_MATER=material,
RESULTAT=resu,
REPE_COQUE=_F(NIVE_COUCHE='SUP',),
OPTION='SIGM_ELNO_DEPL',);
determine stress at outer layer
resuSUP=CALC_ELEM(MODELE=modmod,
CHAM_MATER=material,
RESULTAT=resu,
REPE_COQUE=_F(NIVE_COUCHE='SUP',),
OPTION=('SIGM_ELNO_DEPL','EQUI_ELNO_SIGM',),);
resuSUP=CALC_NO(reuse =resuSUP,
RESULTAT=resuSUP,
OPTION=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM',),);
IMPR_RESU(MODELE=modmod,
FORMAT='MED',
UNITE=80,
RESU=(_F(MAILLAGE=meshmod,
RESULTAT=resu,
NOM_CHAM='DEPL',),
_F(MAILLAGE=meshmod,
RESULTAT=resuSUP,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM',),),),);
FIN();
Postprocessing
displacements
- Deformed shape
Triangle mesh | Hexahedra mesh
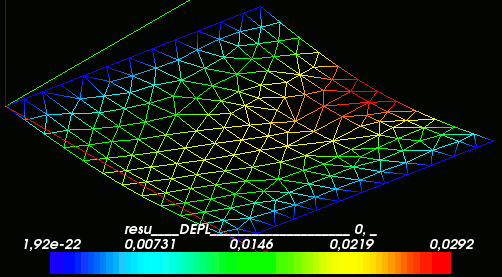
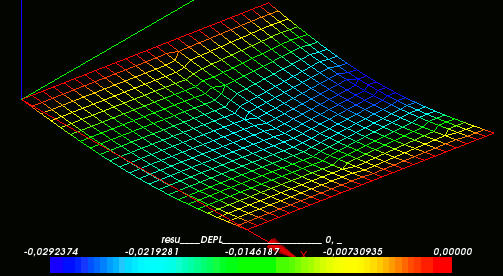
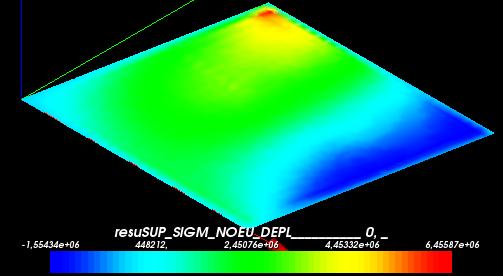
Local stresses at upper layer
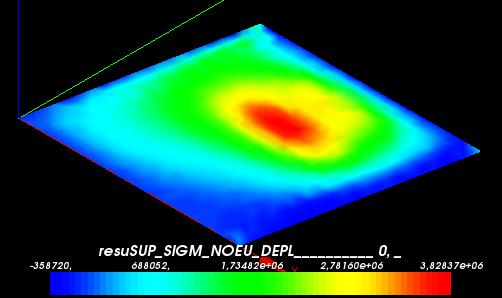
- SIXX
Triangle mesh | Hexahedra mesh


- SIYY
Triangle mesh | Hexahedra mesh
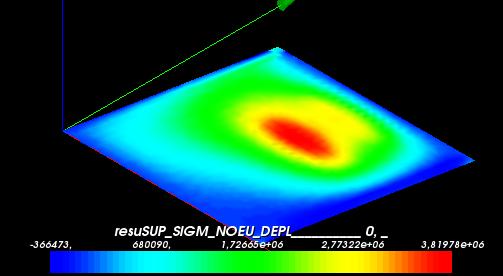
- SIXY
Triangle mesh | Hexahedra mesh
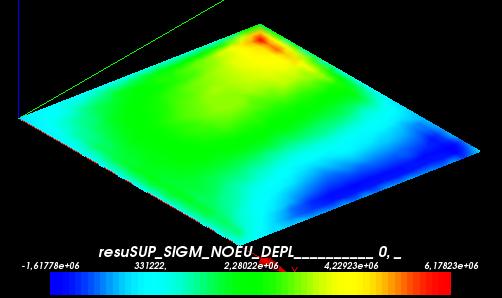
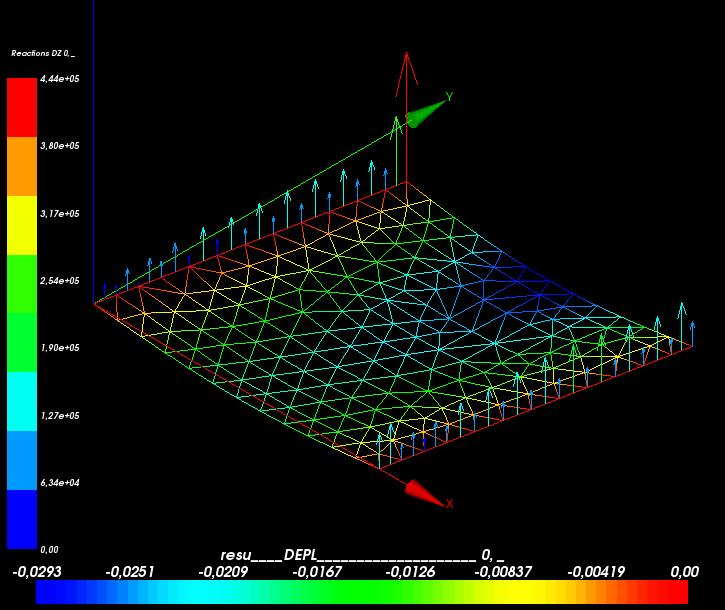
Reactions forces
To write the reaction forces to a med file and display them in Salome you can use:
IMPR_RESU(UNITE=80,
FORMAT='MED',
MODELE=modmod,
RESU=(_F(MAILLAGE=meshmod,
RESULTAT=resu,
NOM_CHAM=('REAC_NODA',),),),);
Note the the pressures have reversed sign here for nicer visual effect.
- Triangle mesh
- Hexahedra mesh
Extraction of maximum displacements and stresses
For more details with respect to reaction forces and moments, nodal forces and extremes of stresses, see this part on tables.
The OPERATION='EXTREMA' calculates the MIN, MAX, MIN_ABS, MAX_ABS values of a requested field on the geometrical area.
See http://www.code-aster.org/V2/doc/v9/man_u/u4/u4.81.21.pdf
TB_nodf=POST_RELEVE_T(ACTION=(_F(OPERATION='EXTREMA',
INTITULE='displacements dz',
RESULTAT=resu,
NOM_CHAM='DEPL',
TOUT_ORDRE='OUI',
GROUP_NO='Nsupport',
NOM_CMP='DZ',),
_F(OPERATION='EXTREMA',
INTITULE='equiss NOEU',
RESULTAT=resuSUP,
NOM_CHAM='EQUI_NOEU_SIGM',
TOUT_ORDRE='OUI',
GROUP_NO='Nsupport',
NOM_CMP=('VMIS','TRESCA','PRIN_1','PRIN_2','PRIN_3',),),
_F(OPERATION='EXTREMA',
INTITULE='equiss ELNO',
RESULTAT=resuSUP,
NOM_CHAM='EQUI_ELNO_SIGM',
TOUT_ORDRE='OUI',
GROUP_NO='Nsupport',
NOM_CMP=('VMIS','TRESCA','PRIN_1','PRIN_2','PRIN_3',),),
_F(OPERATION='EXTREMA',
INTITULE='local stresses',
RESULTAT=resuSUP,
NOM_CHAM='SIGM_NOEU_DEPL',
TOUT_ORDRE='OUI',
GROUP_NO='Nsupport',
NOM_CMP=('SIXX','SIYY','SIXY',),),),
TITRE='Min/max of displacement DZ - stresses',);
#extreme displacements on group allnodes #Min/max of displacement DZ - stresses * INTITULE * RESU * NOM_CHAM * NUME_ORDRE * EXTREMA * MAILLE * NOEUD * CMP * VALE * displacements dz * resu * DEPL * 1 * MAX * - * N241 * DZ * 1.94659E-19 * displacements dz * resu * DEPL * 1 * MIN * - * N115 * DZ * -2.91659E-02 * displacements dz * resu * DEPL * 1 * MAX_ABS * - * N115 * DZ * 2.91659E-02 * displacements dz * resu * DEPL * 1 * MIN_ABS * - * N152 * DZ * 4.74802E-22
* equiss NOEU * resuSUP * EQUI_NOEU_SIGM * 1 * MAX * - * N107 * TRESCA * 1.99754E+07 * equiss NOEU * resuSUP * EQUI_NOEU_SIGM * 1 * MIN * - * N182 * PRIN_1 * -3.00400E+06 * equiss NOEU * resuSUP * EQUI_NOEU_SIGM * 1 * MAX_ABS * - * N107 * TRESCA * 1.99754E+07 * equiss NOEU * resuSUP * EQUI_NOEU_SIGM * 1 * MIN_ABS * - * N35 * PRIN_2 * 1.32964E+03
* equiss ELNO * resuSUP * EQUI_ELNO_SIGM * 1 * MAX * M204 * N107 * TRESCA * 2.02489E+07 * equiss ELNO * resuSUP * EQUI_ELNO_SIGM * 1 * MIN * M125 * N123 * PRIN_1 * -6.08974E+06 * equiss ELNO * resuSUP * EQUI_ELNO_SIGM * 1 * MAX_ABS * M204 * N107 * TRESCA * 2.02489E+07 * equiss ELNO * resuSUP * EQUI_ELNO_SIGM * 1 * MIN_ABS * M69 * NS1 * VMIS * 0.00000E+00
* local stresses * resuSUP * SIGM_NOEU_DEPL * 1 * MAX * - * N107 * SIXX * 1.97055E+07 * local stresses * resuSUP * SIGM_NOEU_DEPL * 1 * MIN * - * N81 * SIXY * -9.99157E+05 * local stresses * resuSUP * SIGM_NOEU_DEPL * 1 * MAX_ABS * - * N107 * SIXX * 1.97055E+07 * local stresses * resuSUP * SIGM_NOEU_DEPL * 1 * MIN_ABS * - * N250 * SIYY * 1.87510E+04
Note that the minimum and maximum values of the local stresses are taken over the complete group denoted by the NOM_CMP=('VMIS','TRESCA','PRIN_1','PRIN_2','PRIN_3',)
So if you want the minimum and maximum values seperately, take only one component for each extration of the extreme values, eg; NOM_CMP='DZ'
Possible error messages
Errors on Converting triangle and quad elements to coque_3d
Conversion of elements that are not available
In the CREA_MAILLAGE command the correct element must be given: convert TRIA6_7 or QUAD8_9. Suppose you have both TRIA6 and QUAD8 elements in the mesh, and the conversion command is:
meshmod=CREA_MAILLAGE(MAILLAGE=meshinit,
MODI_MAILLE=_F(TOUT='OUI',OPTION='TRIA6_7',),);
you get the following error message:
! <EXCEPTION><MODELISA6_96> ! ! les 60 mailles imprimées ci-dessus n'appartiennent pas au modèle et pourtant elles ont ete affectées dans le mot-clé facteur : ! FORCE_COQUE
Solve it by expanding or decreasing the OPTION part, eg:
meshmod=CREA_MAILLAGE(MAILLAGE=meshinit,
MODI_MAILLE=(_F(TOUT='OUI',OPTION='TRIA6_7',),
_F(TOUT='OUI',OPTION='QUAD8_9',),),);
Linear mesh instead of quadratic mesh
When applied to a linear mesh, after the command
meshmod=CREA_MAILLAGE(MAILLAGE=meshinit,
MODI_MAILLE=(_F(TOUT='OUI',OPTION='TRIA6_7',),
_F(TOUT='OUI',OPTION='QUAD8_9',),),);
the following error message is issued:
!----------------------------------------------------------! ! <EXCEPTION> <MODELISA3_32> ! ! ! ! Erreur utilisateur dans CREA_MAILLAGE/MODI_MAILLE : ! ! Vous avez demandé la transformation de type QUAD8_9. ! ! Mais il n'y a aucune maille quadratique à transformer. ! !----------------------------------------------------------!
This one is quite clear!