Contrib:KeesWouters/shell/arlequin
Contents
The connection between shell and solid elements
This part describes the use of the Arlequin method to connect shell and solid elements. Since version CA10.1.19 you can use liaison_mail with TYPE_RACCORD='MASSIF_COQUE'/'COQUE_MASSIF' to interface between the two incompatible elements. I think in most cases this last option is much easier to use. You can also interface between different shell types; for more information see the links at the end of this contribution: liaisonmail
To start with, this contribution mainly focuses on the use of Salome and Code Aster, not on the results and the mechanical justifications of the code that has been used. So no guarantee that the results will be correct up to the fifth decimal place, which they are not. I do hope though that this information is useful. For me it has been, because I had to think about some commands and look through the documentation and learn from that. In case of mistakes, errors or remarks, please notify me, or better, you are invited to correct or edit them yourself. Enjoy.
I stole a lot of ideas from the CaeLinux and Code Aster forums. So thank you for all who posted on this topic.
[As usual, the files that define the geometry, mesh and command files can be found at the end of this contribution.]
The construction
The geometry of the construction
To establish a connection between shell and solid elements the Arlequin method can be used. Later on a comparison with a solid region is given.
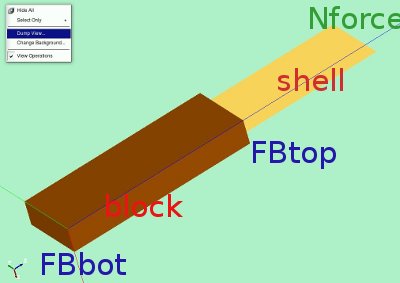
As usual the geometry is quite simple in order not to disturb the issue we would like to show with other difficulties. The first part consists of a beam of height 23 [mm] and a cross section of 3*8 [mm2]. This part is modeled by solid elements. On top of this another beam of height 17 [mm] is added. The width of this beam is 8 [mm]. This part is modeled by shell elements, ie. only the 2D dimensions -height and width- are modeled here. The thickness of 1.5 [mm] (i.e. EPAIS=1.500) is defined in the Aster command file.
The geometry is defined in a python script (for download see end of this contribution) and can be loaded into Salome Geometry module by File --> Load script (or ctrl T in the object browser window). Right click Refresh or push F5 after loading if necessary.
- x direction is out-of-plane of the shell
- z direction is in the main direction of the construction
The mesh of the construction
For the command file in Code Aster we need various parts (or groups in Salome) to apply boundary conditions, forces, material properties and such. These groups are depicted in the image above:
- the bottom and top surface of the block FBbot and FBtop,
- the solid element region block,
- the shell elements shell and
- the two vertices on top edge of the shell elements: Nforce
Again, the mesh of the construction is defined in a python script.
First, a mesh with linear elements has been used (tetra4 and tria3 elements) that can be used with DKT modelisation. Later a quadratic mesh with tetra10 and tria6 elements has been employed. This will provide us with a better converging solution, but makes the command file a bit more complex because we need to modify the tria6 to a tria7 mesh for coque_3d finite elements. The coque_3d element has an extra node at the its centre.
Relevant part of the command file
The boundary conditions are applied on FBbot: all displacements of this surface are restricted. The forces are applied on the two nodes Nforce in the out-of-plane or x direction and the magnitude is 10 N each, ie. 20 N in total. The material properties of both the shell and solid elements are steel.
In the command file this results in:
SVmodel=AFFE_MODELE(INFO=1,
MAILLAGE=SVmesh,
AFFE=(_F(GROUP_MA='block',
PHENOMENE='MECANIQUE',
MODELISATION='3D',),
_F(GROUP_MA='shell',
PHENOMENE='MECANIQUE',
MODELISATION='DKT',),),);
Shell=AFFE_CARA_ELEM(INFO=2,MODELE=SVmodel,
COQUE=_F(GROUP_MA='shell',
EPAIS=1.500,
VECTEUR=(0,1,0),); # defines local x-axis of shell, default global x-axis
Steel=DEFI_MATERIAU(ELAS=_F(E=210000,NU=0.3,),);
Mat=AFFE_MATERIAU(MAILLAGE=SVmesh,
AFFE=_F(GROUP_MA=('block','shell',),
MATER=Steel,),);
The Arlequin method
The Arlequin connection
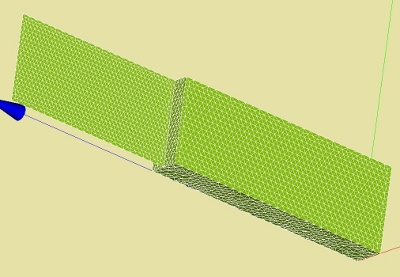
The Arlequin method requires two regions where the interaction between the parts take place. In this case between the solid element group block and the shell elements shell.
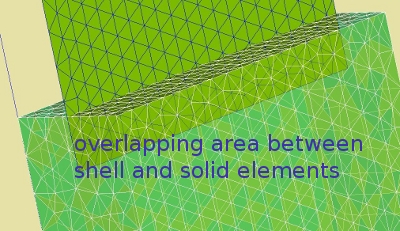
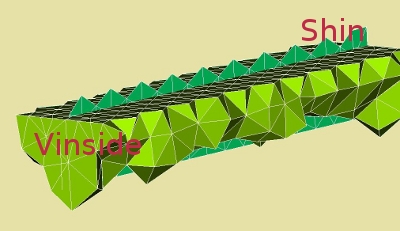
The part of the interaction of the block elements are grouped together in Vinside and the shell elements in Shin. In the images below regions are depicted. Keep in mind that there needs to be an overlap between the two parts to be able to interact *). In this case the shell elements dive into the solid elements for 1.2 [mm].
In these two images the interaction area of the shell and solid elements are given:
- the shell elements -Shin- and
- the solid elements -Vinside-
The Arlequin method is defined in the AFFE_CHAR_MECA, where also the boundary conditions and forces acting on the construction are defined. The main parameters of the command are the MODELE and the parameters for the definition of the 'forces', in this case DDL_IMPO and FORCE_NODALE. ARLEQUIN takes the two interacting groups GROUP_MA_1 and GROUP_MA_2, the GROUP_MA_COLL. In case of shell elements also the CARA_ELEM=Shell needs to be provided. Finally COLLAGE and POIDS may be added.
force=AFFE_CHAR_MECA(MODELE=SVmodel,
DDL_IMPO=_F(GROUP_MA='FBbot',
LIAISON='ENCASTRE',),
FORCE_NODALE=_F(GROUP_NO='Nforce',
FX=10.00,),
ARLEQUIN=_F(GROUP_MA_1='Shin',
GROUP_MA_2='Vinside',
GROUP_MA_COLL='Vinside',
CARA_ELEM=Shell,
COLLAGE='GROUP_MA_1',
POIDS_1=0.99,),);
Note that:
- GROUP_MA_1 and GROUP_MA_2 need to have an overlapping region
- GROUP_MA_1 and GROUP_MA_2 have exactly the same weight, they can be interchanged
- POIDS is a number between 0.0 and 1.0
- GROUP_MA_COLL is one of either GROUP_MA_1 and GROUP_MA_2
- [still need to figure out what is the exact meaning of these last keywords.]
The forces then being applied by the MECA_STATIQUE command:
SVresult=MECA_STATIQUE(MODELE=SVmodel,
CHAM_MATER=Mat,
CARA_ELEM=Shell,
EXCIT=_F(CHARGE=force,),);
*) If no interaction between the parts take place, Code Aster will respond with ! <EXCEPTION> <ARLEQUIN_9> ! ! Les deux domaines ne se recouvrent pas. Vérifiez vos groupes. !
in the error and messages files.
This message:
! <EXCEPTION> <ARLEQUIN_14> ! ! La zone de superposition des modèles dans Arlequin ne contient aucune maille !
is issued when eg. there is only line contact of the shell and the solid elements regions.
The determination of the Arlequin regions
We need to define two regions in the contact area for the solid and shell elements. In principle this can be done by several methods, one of them being picking all the elements or using filters in the mesh module of Salome. Picking all the elements is troublesome and therefor not generally advisable. The use of filters I did not really try so far. So I tried using some python script as an alternative.
Alternatively, if one had constructed the geometry of the solid and the shell using partitioning and appropriate node/element groups are defined during the meshing process, then those groups can become the basis for defining the two ARLEQUIN regions.
The general idea is to determine the nodes in the contact areas and then searching for solid or shell elements that have nodes in the selected region. For this we use some python scripts.
Numeric has been imported for some matrix calculations. [It would have been much easier if I got Numpy working for some calculations, but alas....]
The python script for selecting the elements
Selecting the elements for the Arlequin method
First, create a list of all elements with type FACES -2D elements- and VOLUME -3D elements by the geompy command from the mesh constr:
- list_of_faces = constr.GetElementsByType(FACE)
- list_of_volumes = constr.GetElementsByType(VOLUME)
This list_of_faces now contains all the 2D elements within in the mesh constr. The list_of_volumes contains all 3D elements.
Then determine nodes near the shell area in the contact zone: this area is restricted by a block defined with two vertices b1 and b2:
- b1 = Numeric.array([0.495*Bx,0.01*By,Bz-2.000]) # min block, xyz_min
- b2 = Numeric.array([0.505*Bx,0.99*By,Bz-0.010]) # max block, xyz_max
where [Bx, By, Bz] is one of the vertices of the solid element region block, the other one is [0, 0, 0].
The nodes within this block are determined by
- Bnin,Bnout = node_group_within_block(constr,b1,b2)
with parameters for the mesh constr and the definition of the block (b1, b2). The output are the nodes inside and outside the provided block, Bnin and Bnout respectively. The function element_on_nodes then picks the shell elements (with geompy type FACE) having nodes within the requested area:
- Shin = element_on_nodes(constr,list_of_faces,Bnin).
The input parameters are the mesh constr, the 2D elements list_of_faces and the previously determined nodes Bnin.
To group these elements in the mesh object browser we use
- grp = constr.CreateEmptyGroup(FACE, "Shin")
- grp.Add(Shin)
where the group Shin now can be used within the Aster command files.
Selecting the elements for the solid area
For the nodes in the solid area we determine the nodes near the intersection line of the shell and block region. This line is determined by the end vertices p1 and p2. The nodes within a radius of VRadius are selected and stored in Vnodesin by the function:
- Vnodesin,Vnodesout = node_group_near_line(constr,p1,p2,VRadius)
To select all volumes near the line L(p1, p2) again we use
- Vinside = element_on_nodes(constr,list_of_volumes,Vnodesin)
now using the list with volume elements list_of_volumes.
Grouping them together for use within Salome of Aster command file again:
- grp = constr.CreateEmptyGroup(VOLUME, "Vinside")
- grp.Add(Vinside)
In this picture the nodes for the shell and solid elements are given (view to the xz plane). The vertical white line denotes the selected shell elements Shin.
Note:
- Full details are in the python script, at the end of this contribution.
- This method cannot be used generally if more complex interaction regions need to be addressed, but then you could address this problem in Salome directly by defining the regions there, as described earlier.
Applying a solid region to connect two regions
The solid node region
Instead of selecting two contact areas, it is also possible to define a solid region in the intersection area of the shell and block. The disadvantage of this method is that the complete interaction region behaves as one rigid block and therefore might introduce additional stiffness and stresses. So in general I think this method is not advisable.
In order to introduce the method, a gap of 0.1 [mm] between the shell and block area is defined. The nodes on the bottom edge of the shell are selected as well as the inner nodes on the top surface FBtop of the block, see image below. The selection is done by the python function mentioned in the Arlequin method.
Note that the gap of 0.1 [mm] can easily be reduced to 0. Then this method has the advantage that in general less modification of a CAD file needs to be made for further processing with eg Aster.
Because the shell nodes have 6 degrees of freedom, including rotations, one row of nodes for the shell elements are enough to constrain the displacements and rotations of the shell. For the solid elements the restriction for rotation must be obtained from nodes that can introduce a moment by two opposite forces and the distance between them.
The Aster command
In the AFFE_CHAR_MECA model the Arlequin key word is now replaced by LIAISON_SOLIDE:
force=AFFE_CHAR_MECA(MODELE=SVmodel,
DDL_IMPO=_F(GROUP_MA='FBbot',LIAISON='ENCASTRE',),
FORCE_NODALE=_F(GROUP_NO='Nforce',FX=10.00,),
LIAISON_SOLIDE=_F(GROUP_NO='Nsolid',),);
The other part of the command file remains as is.
Errors for the quadratic mesh
In case you apply a quadratic mesh for DKT shell elements, the following error messages are given in the mess file:
! <EXCEPTION> <MODELISA_30> ! ! vous ne pouvez affecter des valeurs de type "COQUE" au modèle LINmodel ! ! qui ne contient pas un seul élément coque !
! <EXCEPTION> <MODELISA5_57> ! ! erreur(s) rencontree(s) lors de la verification des affectations. !
The quadratic -coque_3d- elements
In stead of the DTK modelisation with linear elements we will now switch to a quadratic mesh with coque_3d finite elements. In the Python mesh file a few lines need to be added to provide a quadratic mesh or use the modification --> convert to/from quadratic command in the mesh module of Salome. After LIRE_MAILLAGE the command for converting the mesh suitable for coque_3d elements are added (see remark for use of CA10+):
COQmesh=CREA_MAILLAGE(MAILLAGE=LINmesh,
MODI_MAILLE=(_F(TOUT='OUI',OPTION='QUAD8_9',),
_F(TOUT='OUI',OPTION='TRIA6_7',),),);
and the AFFE_MODELE now changes to:
COQmodel=AFFE_MODELE(INFO=1,
MAILLAGE=COQmesh,
AFFE=(_F(GROUP_MA=('block',),
PHENOMENE='MECANIQUE',
MODELISATION='3D',),
_F(GROUP_MA=('shell',),
PHENOMENE='MECANIQUE',
MODELISATION='COQUE_3D',),),);
and the remaining part is practically the same.
The results
Arlequin - The displacements of the top vertices
Applying the 10 N in the out-of-plane direction on the top vertices yields a displacements of 0.344 [mm]. The results are written in to text file, to unit 26, type mast, defined in the ASTK window.
The commands to write the results to a text file are:
TB_nodf=POST_RELEVE_T(ACTION=(_F(OPERATION='EXTRACTION',
INTITULE='displacements',
RESULTAT=SVresult,
NOM_CHAM='DEPL',
TOUT_ORDRE='OUI',
GROUP_NO='Nforce',
RESULTANTE=('DX','DY','DZ',),
#NOM_CMP=('DX','DY','DZ',),
MOYE_NOEUD='NON',),),
TITRE='displacements of top vertices',);
IMPR_TABLE(TABLE=TB_nodf,
FORMAT='TABLEAU',
UNITE=26,
SEPARATEUR=' * ',
TITRE='displacements at nodes on group Nforce',);
And the content of the resulting text file:
#displacements at nodes on group Nforce #displacements of top vertices * INTITULE * RESU * NOM_CHAM * NUME_ORDRE * INST * DX * DY * DZ * displacements * SVresult * DEPL * 1 * 0.00000E+00 * 6.88544E-01 * -2.57008E-05 * 2.80473E-06
Remarks:
- - For this set of commands, the sum of the displacements (resultante) of the two nodes is given.
- - Reducing the overlapping area between the shells and solids yields a x displacement of 0.757891/2 ~ 0.379 [mm].
Solid region - The displacements of the top vertices
- The results of the linear mesh (DKT shell elements)
In this case -with a gap between the shell and solid elements of 0.1 [mm]- the displacement at the top is 0.334 [mm]. The results text file:
#displacements at nodes on group Nforce #displacements of top vertices * INTITULE * NOEUD * RESU * NOM_CHAM * NUME_ORDRE * INST * ABSC_CURV * COOR_X * COOR_Y * COOR_Z * DX * DY * DZ * displacements * N1 * LINres * DEPL * 1 * 0.00000E+00 * 0.00000E+00 * 1.50000E+00 * 8.00000E+00 * 4.00000E+01 * 3.34314E-01 * 2.38140E-05 * -2.53450E-06 * displacements * N4 * LINres * DEPL * 1 * 0.00000E+00 * 8.00000E+00 * 1.50000E+00 * 0.00000E+00 * 4.00000E+01 * 3.34305E-01 * 2.38140E-05 * 8.23189E-06
Remark: reducing the gap between the shell and the block to 0 [mm] yields a displacement of 0.668618/2 ~ 0.334 mm.
- The results of the quadratic mesh (COQUE_3D shell elements)
The displacement at the top is now 0.348 [mm] or 4 % more. The content of the results text file is here [RESULTANTE=('DX') has been changed to NOM_CMP=('DX') to write the displacements of all nodes]:
#displacements at nodes on group Nforce #displacements of top vertices *INTITULE * NOEUD * RESU * NOM_CHAM * NUME_ORDRE * INST * ABSC_CURV * COOR_X * COOR_Y * COOR_Z * DX *displacements * N1 * COQres * DEPL * 1 * 0.00000E+00 * 0.00000E+00 * 1.50000E+00 * 8.00000E+00 * 4.00000E+01 * 3.48162E-01 *displacements * N4 * COQres * DEPL * 1 * 0.00000E+00 * 8.00000E+00 * 1.50000E+00 * 0.00000E+00 * 4.00000E+01 * 3.48217E-01
Using LIAISON_MAIL
Since C_Aster version10.1.19??? (ckeck) it is possible to connect solid-shell, shell-shell directly by LIAISON_MAIL. No interconnecting regions are needed then as in Arlequin. For more details look [here ....(tbd)]. Here are some first results:
- For Liaison_mail with linear elements (DKT)
#displacements at nodes on group Nforce #displacements of top vertices * INTITULE * NOEUD * RESU * NOM_CHAM * NUME_ORDRE * INST * ABSC_CURV * COOR_X * COOR_Y * COOR_Z * DX * DY * DZ * displacements * N3494 * SVresult * DEPL * 1 * 0.00000E+00 * 0.00000E+00 * 1.50000E+00 * 8.00000E+00 * 4.00000E+01 * 3.27736E-01 * 1.19326E-05 * 1.60472E-06 * displacements * N5015 * SVresult * DEPL * 1 * 0.00000E+00 * 8.00000E+00 * 1.50000E+00 * 0.00000E+00 * 4.00000E+01 * 3.27709E-01 * 1.19330E-05 * 5.41754E-06
The images - Arlequin
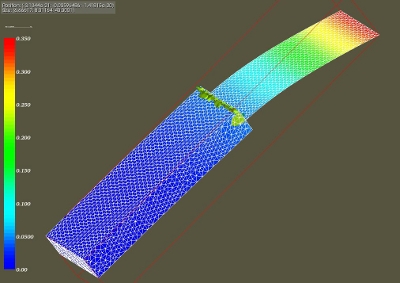
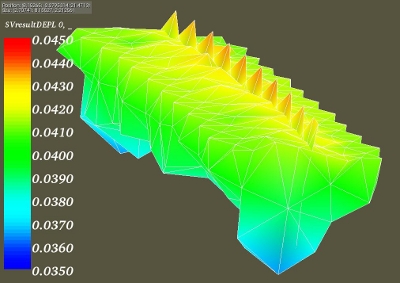
And finally here are some pictures of the displacements field. All images show the x displacements on the deformed shape.
- top: displacements field of the block and shell regions, including the undeformed Arlequin regions Vinside and Shin
- bottom left: displacement field of block and shell regions near the Arlequin intersection, surfaceframe
- bottom right: displacement of the Arlequin regions
The images - Solid region
- left, overall view of x displacement
- right, detail of the 'contact' area with the solid nodes region offset
Download files
- This zip contains the following files for the Arlequin method:
- BSgeomesh_arleq5N.py python geometry and mesh files (load in Salome by File --> Load script (cntrl T)) and right select refresh (F5) in the object browser). Export the mesh constr in the mesh module to constrlin.med for further processing by Code-Aster, controlled by ASTK.
- arlequin3.comm command files for Code-Aster
- astk file for file control by ASTK
- tabres1.txt, text file with nodal displacements of nodes Nforce.
- The result file con2res.med can be viewed in the post processor module of Salome by File --> Import --> con2res.med or cntrl I in the object browser.
- See above, using LIAISON_SOLIDE method; region with solid nodes.
- In Salome Object Browser right click on the mesh and Export to MED file with file name constrlin.med
Remarks - quadratic elements with Arlequin - links
- Code Aster versions 9.2 and up are capable of using quadratic elements with the Arlequin method. See:
- Use of LIAISON_MAIL: Since 10.1.19, you have a new functionality in LIAISON_MAIL which is detailed here : (fiche 13381)
- More information about the Arlequin method can be found here:
- http://www.code-aster.org/V2/doc/default/man_u/u4/u4.44.01.pdf, page 71/75, the AFFE_CARA_ELEM command
- http://www.code-aster.org/V2/doc/default/man_r/r3/r3.03.08.pdf
- http://www.code-aster.org/V2/doc/default/man_u/u4/u4.44.01.pdf, page 71/75, the AFFE_CARA_ELEM command
That's it for now
Any comments?
Kees