Difference between revisions of "Contrib:KeesWouters/bc/rbe3"
Keeswouters (Talk | contribs) m (→Boundary conditions) |
Keeswouters (Talk | contribs) m (→Results of various loads and connections) |
||
| Line 150: | Line 150: | ||
=='''Results of various loads and connections'''== | =='''Results of various loads and connections'''== | ||
Both the results for the symmetric and asymmetric mesh will be shown. | Both the results for the symmetric and asymmetric mesh will be shown. | ||
| + | The three different methods to apply the load are shown in order: | ||
| + | * applying a distributed torque on the axial face | ||
| + | * applying a torque to the master node connected by 'beam' connection | ||
| + | * applying a torque to the master node by RBE3 connection | ||
==='''Applying a distributed torque on the axial face'''=== | ==='''Applying a distributed torque on the axial face'''=== | ||
Revision as of 10:45, 12 March 2016
Contents
- 1 Purpose of the RBE3 constraint
- 2 Geometry and mesh of the block with cylindrical hole
- 3 Definition of node groups
- 4 Definition of solid and discrete model
- 5 Boundary conditions
- 6 Coupling methods
- 7 Results of various loads and connections
- 8 Reaction forces - older model
- 9 Input files for the FE Analysis and references
Purpose of the RBE3 constraint
[under construction]
RBE3
RBE3 defines a constraint relation in which the motion of a reference grid point is the least square weighted average of the motion at other grid points. The element is useful for beaming loads and masses of a reference point to a set of grid points
(from [[1]] NX Nastran Element Library Reference.
See also this [[2]link.]
A RBE3 constraint maybe useful, amongst others:
- to distribute a load to a set of nodes without the need of a rigid body constraint or
- to connect different bodies to each other without generating additional rigid body constraints.
Edit:
Apart from a RBE3 constraint it is possible to use a LIAISON_ELEM with OPTION='3D_POU' to connect one master node to a set of nodes without applying additional rigid body constraints. This has been added later in this contribution.
On a cylinder, we will show the results of a torque applied to the bottom axial area for two mesh types (symmetric and asymmetric in tangential direction). The torque will be applied in three different ways:
- direct distribution of the torque on the axial face by tangential forces on the nodes
- apply a torque on a master node and define a connection by
- a master node from a 'beam' to the axial face and
- RBE3 from the master to the axial face.
The results are obtained by the ParaViz module.
Geometry and mesh of the block with cylindrical hole
This contribution shows the behaviour of the RBE3 constraint. In this case it is used to apply a moment to the top surface of a cylinder. The bottom surface of the cylinder is fixed 3dof to the world. The inner and outer diameters of the cylinder are 15 and 17 (arbitrairy units) and length 75. The material is steel, material properties are in ISO units (this makes the dimensions of the cylinder ISO as well).
The geometrical entities on the cylinder are, A for surface areas:
- Atop and
- Abot
Abot, at z=0, is used to apply the torsion moment. Atop, at z=75, is used to apply the fixed boundary condition to the 'world'. Two types of mesh have been used to show the effect of the rbe3 behaviour. Mesh 1 is symmetric whereas mesh 2 is asymmetric in tangential direction. All elements are quadratic hex elements.
- in axial direction 12 elements are present.
- in radial direction 3 elements are present.
- in tangential direction:
- in quadrants 2 and 3: 23 elements are present (-y direction)
- in quadrants 1 and 4, (+y direction):
- mesh type 1: 23 elements are present (see figure left)
- mesh type 2: 7 elements are present (see figure right)
- The centre 0D node Nmaster is the master node to apply the constraint to the axial surface.
Definition of node groups
In order to apply correct boundary conditions and loads on the bottom and top axial surfaces, we need to convert the groups to nodes (GROUP_MA --> GROUP_NO) using the following commands:
Mcyl=DEFI_GROUP(reuse =Mcyl,
MAILLAGE=Mcyl,
CREA_GROUP_NO=_F(NOM='Nbot',GROUP_MA='Abot',),);
Mcyl=DEFI_GROUP(reuse =Mcyl,
MAILLAGE=Mcyl,
CREA_GROUP_NO=_F(NOM='Nmaster',GROUP_MA='Pmaster0',),);
Definition of solid and discrete model
The master node apparently does not have any degrees of freedom, so we need to apply a discrete element MODELISATION='DIS_TR' to the master node Pmaster. This is an element that carries mass and stiffness, but all entities have been set to zero in the value assignment, see DISCRET and VALE in the statement below. Then effectively only a node with translational and rotational degrees of freedom remains. This is just a trick to be able to apply a torque on this node.
CylModel=AFFE_MODELE(MAILLAGE=Mcyl,
AFFE=(_F(TOUT='OUI',
PHENOMENE='MECANIQUE',
MODELISATION='3D',),
_F(GROUP_NO='Nmaster',
PHENOMENE='MECANIQUE',
MODELISATION='DIS_TR',),),);
N_stmass=AFFE_CARA_ELEM(MODELE=CylModel,
INFO=2,
DISCRET=(_F(CARA='M_TR_D_N',
GROUP_NO='Nmaster',
VALE=[0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.00,0.00,0.00]),
_F(CARA='K_TR_D_N',
GROUP_NO='Nmaster',
VALE=[0.0,0.0,0.0,0.0,0.0,0.0]),),);
The command DISCRET_F(CARA='M_TR_D_N',GROUP_NO='Nmaster',VALE=[0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.00,0.00,0.00]), defines:
- the mass properties M_TR_D_N for
- the node 'Nmaster' (a single node need to be applied to the GROUP_NO), and
- the VALE group defines the mass m and Ixx, Iyy, Izz, Ixy, Iyx and Izx and three eccentricities:
- VALE=[m,Ixx,Iyy,Izz,Ixy,Iyz,Izx,Ecx,Ecy,Ecz]
The command DISCRET_F(CARA='K_TR_D_N',GROUP_NO='Nmaster',VALE=[0.0,0.0,0.0,0.0,0.0,0.0]), defines:
- the stiffness properties K_TR_D_N for
- the node 'Nmaster' (a single node may to be applied to the GROUP_NO), and
- the VALE group defines the stiffnesses Kx, Ky, Kz, Krotx, Kroty and Krotz, all set to zero:
- VALE=[Kx,Ky,Kz,Krotx,Kroty,Krotz]
Boundary conditions
The easiest way to connect the top face to the fixed world is to just use an DDL_IMPO command and fix the nodes of this face 3DOF (translations x, y and z). This however, introduces local stresses at the outer end of the cylinder.
Coupling methods
Coupling between a node of a beam and 3D face by 3D_POU
The coupling between a line element and a massive 3D body can be achieved by the LIAISON_ELEM with OPTION='3D_POU'. The nice part here is that the line part may be degradated to a single node. Normally you should select a node of a beam element and the nodes of the connecting face of the 3D body that link to each other. Here we select the master node Nmaster as GROUP_NO_2 and the axial, bottom face as GROUP_MA_1. In detail the command is:
node3D=AFFE_CHAR_MECA(INFO=1,
MODELE=CylModel,
LIAISON_ELEM=_F(GROUP_MA_1='Abot',
GROUP_NO_2='Nmaster',
OPTION='3D_POU'),);
Mmaster=AFFE_CHAR_MECA(MODELE=CylModel,
FORCE_NODALE=_F(GROUP_NO='Nmaster',MZ=1000,),);
result=MECA_STATIQUE(MODELE=CylModel,
CHAM_MATER=AssyMat,
CARA_ELEM=N_stmass,
EXCIT=(_F(CHARGE=fixbc,),
_F(CHARGE=fixcyl,), ## bc: fixcyl / fixbc / fixNmast
_F(CHARGE=Mmaster), ## load: Tmaster / Ftorsion
_F(CHARGE=node3D),),) ## connection: node3D / nodeRBE3
The second AFFE_CHAR_MECA applies a torque of 1000 around the z axis on the master node Nmaster. This torque will be distributed on the nodes of the face defined by Abot without any additional stiffness.
Coupling the node by RBE3
coupling between a node and 3D face by RBE3.
The first AFFE_CHAR_MECA command defines the RBE3 constraint between the master node 'Nmaster' and the slave nodes 'Nbot'. The nodes 'Nbot' are attached to the geometrical entity GROUP_MA='Abot', by the DEFI_GROUP command. The second AFFE_CHAR_MACE command is used to apply the torsion moment MZ equal to 1000 (let say [Nm], if we effectively state that all dimensions are in [m], forces in [N] and pressures and Youngs' modulus in [Pa]).
The degrees of freedom that need to be transferred to the master node Nmaster are given by the values after DDL_MAIT. In this case 6 dofs ('DX','DY','DZ','DRX','DRY','DRZ') are requested and needed because of the mass and stiffness attached to the master node. These degrees of freedom are derived from the degrees of freedom of the group of slave nodes DDL_ESCL='DX-DY-DZ'. The user must take care that the requested dofs on the master can be derived from the degrees of freedom of the slave nodes. The coefficient COEF_ESCL=1 is equal to the number of .... (tbd).
nodeRBE3=AFFE_CHAR_MECA(MODELE=CylModel,
LIAISON_RBE3=_F(GROUP_NO_MAIT='Nmaster',
DDL_MAIT=('DX','DY','DZ','DRX','DRY','DRZ',),
#DDL_MAIT=('DRZ',),
GROUP_NO_ESCL='Nbot',
DDL_ESCL='DX-DY-DZ',
COEF_ESCL=1,),);
torsion=AFFE_CHAR_MECA(MODELE=CylModel,
FORCE_NODALE=_F(GROUP_NO='Nmaster', MZ=1000,),);
Mmaster=AFFE_CHAR_MECA(MODELE=CylModel,
FORCE_NODALE=_F(GROUP_NO='Nmaster',MZ=1000,),);
result=MECA_STATIQUE(MODELE=CylModel,
CHAM_MATER=AssyMat,
CARA_ELEM=N_stmass,
EXCIT=(_F(CHARGE=fixbc,),
_F(CHARGE=fixcyl,), ## bc: fixcyl / fixbc / fixNmast
_F(CHARGE=Mmaster), ## load: Tmaster / Ftorsion
_F(CHARGE=nodeRBE3),),) ## connection: node3D / nodeRBE3
Results of various loads and connections
Both the results for the symmetric and asymmetric mesh will be shown. The three different methods to apply the load are shown in order:
- applying a distributed torque on the axial face
- applying a torque to the master node connected by 'beam' connection
- applying a torque to the master node by RBE3 connection
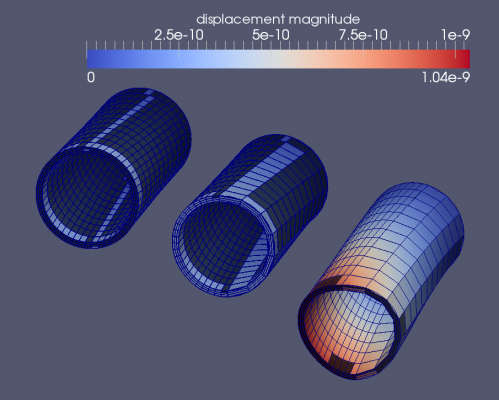
Applying a distributed torque on the axial face
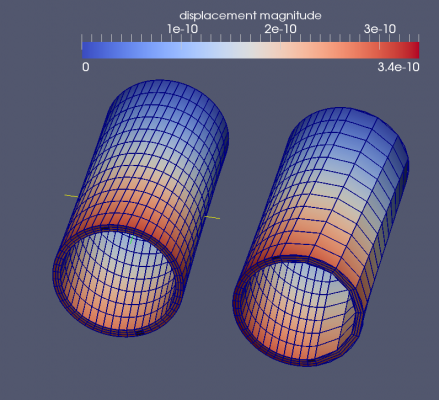
In the picture below the displacement of the cylinder is shown. The left cylinder has a symmetrical mesh (23x23 tangential) and the right picture is asymmetrical meshed (7x23). Both cylinder have roughly the same rotation at the bottom axial plane: the displacement in tangential direction is of the order of 3.1e-10.
For the asymmetric mesh (7x23) a slight asymmetry for the results occur on the axial bottom face. In x-direction an asymmetry is present [dxmin, dxmax] = [-3.3, +2.7]*e-10. In y direction this is symmetric: [dymin, dymax] = [-3.1, +3.1]*e-10.
*
In the picture below, at the right most tube with asymmetric mesh, the torque has applied without notice of the front element size. Each node on the axial face has the same magnutide for the force. The direction is of course always in tangential direction. The load is not a nicely distributed torque. At the -y direction the force is much too high and is not compensated by the force at the +y axis. The total torque around the origin is still -1000 [Nm] though. The corresponding displacements are: x-direction [dxmin, dxmax] = [-10.4, +0.0]*e-10; in y direction [dymin, dymax] = [-3.1, +3.1]*e-10.
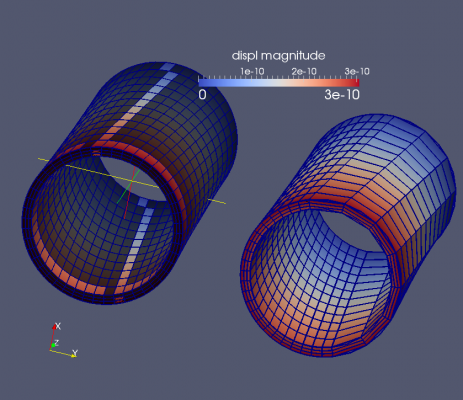
Applying a distributed torque by beam node
In the picture the rotation of the cylinder is nicely visible. The torque is applied on the master node in the centre of the bottom axial face. It is a single node of a virtual beam element that connects to the bottom axial face of the cylinder by the LIAISON_ELEM command and the OPTION='3D_POU'. Both the meshes show exactly the same behaviour. The minimum and maximum displacements at of the cylinder are equal in x and y direction: [dxmin, dxmax] = [dymin, dymax] = [-3.1, +3.1]e-10. Nice behaviour.
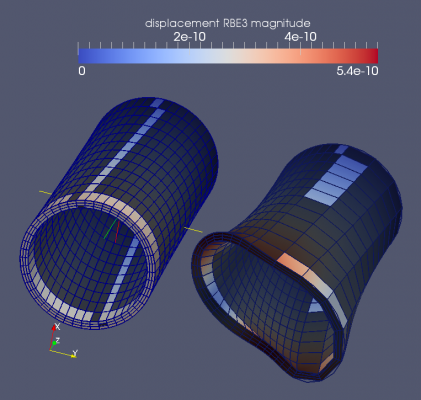
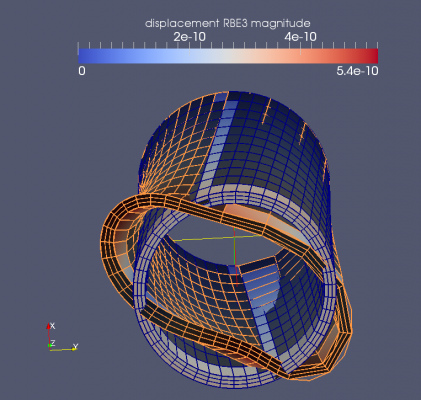
Applying a distributed torque by RBE3
Applying the torque by a RBE3 constraint poses no problem for the symmetric mesh (figure below, left). The asymmetric mesh, however, does not behave as expected. The distribution of the forces is probably not as it should be and the axial face is distorded. Away from this local disturbance the overall deformation is the same as for the symmetric mesh (figure below, right, slant of the mesh in axial direction is the same for both meshes).
Reaction forces - older model
[to be updated]
Here the results are a bit disappointing. The circulair front face is much distorted by the distributed force on the asymmetric mesh.
The reaction forces on the outer edge of the front face (Fx, Fy and the vector value) show that the vector value of the reaction forces are slightly less on the dense mesh (negative x part) compared to the coarse mesh side (positive x part). I would however expect that the reaction would deviate roughly by a factor 2 because of mesh density.
Input files for the FE Analysis and references
to be updated ...
Input files for the asymmetric mesh:
- *.py basicly creates the geometry and mesh suitable for the RBE3 constraint. The additional node and master nodes is also created here, although it gives a warning in Salome
- load by File --> load script (cntrl T in the object browser), refresh (F5) after running
- Save the mesh file by right clicking in the object browser by right clicking on the mesh name Mbcyl; select Export to MED and accept or change the default values
- load by File --> load script (cntrl T in the object browser), refresh (F5) after running
- ASTK file (*.astk, you need to edit the paths to your requirements ...)
- command file (cylinder_e.comm)
Download the files here:
Reference:
[yyyyyyyy, page zz/109]