Contrib:KeesWouters/dynamicload
Contents
- 1 Dynamic analysis of an axial loaded cylinder
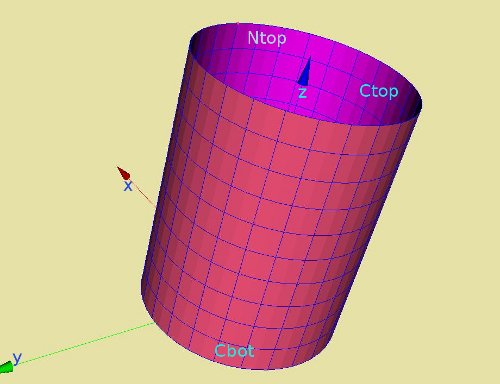
- 2 Geometry of the construction
- 3 Boundary condition and load
- 4 Detailed commands of the applied load
- 5 Defining the solution process
- 6 Results
- 6.1 Writing displacements of a single node
- 6.2 Axial mode shape
- 6.3 Time domain response - no damping
- 6.4 Applying viscous damping proportional to stiffness and mass matrices
- 6.5 Damping proportional to the stiffnes matrix
- 6.6 Damping proportional to the mass matrix
- 6.7 Rayleigh damping - alpha and beta
- 6.8 The bode plot for Rayleigh damping
- 6.9 Influence of resonance frequency on 'mass' damping
- 7 Download files
- 8 References
Dynamic analysis of an axial loaded cylinder
[nearly finished now, could be useful ... ]
To start with, this contribution mainly focuses on the use of Salome and Code Aster, not on the results and the mechanical justifications of the code that has been used. So no guarantee that the results will be correct up to the fifth decimal place, which they are not. I do hope though that this information is useful. For me it has been, because I had to think about some commands and look through the documentation and learn from that. In case of mistakes, errors or remarks, please notify me, or better, you are invited to correct or edit them yourself. Enjoy.
[As usual, the files defining geometry, mesh and command files can be found at the end of this contribution.]
Geometry of the construction
The geometry is based on this contribution. Only the mesh is much coarser to limit calculation time.
Boundary condition and load
The boundary conditions and the loads are the same as defined here. The axial load of 5500 [N] is applied on the top edge of the cylinder. A scaling factor is applied by the function MULT_FONCT in the command DYNA_LINE_TRAN. This scaling factor is zero for the first 2 ms, and goes to unity within a very small time scale, ie. small compared to the resonance frequencies of the axial modes of the cylinder. The scale factor remains unity until the end of the calculation at 40 ms.
Detailed commands of the applied load
The AFFE_CHAR_MECA defines the boundary conditions at the bottom of the cylinder: all dofs are restricted. At the top an axial force is applied with a total force of 5500 N, devided over the circumference of the cylinder.
# define BC and loads # geometry of cylinder for applying loads th = 0.10 # [mm] thickness of shell dcyl = 4.00 # [mm] diameter of cylinder pie = math.pi Lcyl = pie*dcyl # [mm] circumference of the cylinder Fax = 5500.0 # [N] total axial force
clamp=AFFE_CHAR_MECA(MODELE=modelc,
DDL_IMPO=(_F(GROUP_MA=('Cbot'),
DX=0.0,
DY=0.0,
DZ=0.0,
DRX=0.0,
DRY=0.0,
DRZ=0.0,),
_F(GROUP_MA=('Ctop'),
DX=0.0,
DY=0.0,
DRX=0.0,
DRY=0.0,
DRZ=0.0,),),
FORCE_ARETE=_F(GROUP_MA='Ctop',FZ=+Fax/Lcyl,),);
......
A time step is defined by the DEFI_LIST_REEL command. The scaling function castle is defined by the DEFI_FONCTION command. In total tsteps (400) output times will be generated.
# The load will be applied in steps defined by a 'time' function and
# multiplification factor on the load.
tsteps = 400
to = 0.000
tc = 0.002
t1 = (1+1e-5)*tc
te = 0.040
time=DEFI_LIST_REEL(DEBUT=0.0,
INTERVALLE=_F(JUSQU_A=te,NOMBRE=tsteps,),
INFO=2,TITRE='time',);
castle=DEFI_FONCTION(NOM_PARA='INST',
VALE=(to, 0.00,
tc, 0.00,
t1 , 1.00,
te, 1.00,),
INFO=2,TITRE='castle',);
Defining the solution process
We define the dynamic load and solution process by the DYNA_LINE_TRAN command. But first we need to determine the stiffness, mass and damping matrix, ordered according to the dofs by the MACRO_MATR_ASSE command.
MACRO_MATR_ASSE(MODELE=modelc,
CHAM_MATER = matprops,
CARA_ELEM = shellch,
CHARGE = clamp,
NUME_DDL = CO('nddl'),
MATR_ASSE =(_F(MATRICE=CO('Mstiff'),OPTION='RIGI_MECA',),
_F(MATRICE=CO('Mmasse'),OPTION='MASS_MECA',),
_F(MATRICE=CO('Mdampg'),OPTION='AMOR_MECA',),),);
Rdyn = DYNA_LINE_TRAN(MODELE=modelc,
CHAM_MATER= matprops,
CARA_ELEM = shellch,
MATR_MASS = Mmasse,
MATR_RIGI = Mstiff,
MATR_AMOR = Mdampg,
NEWMARK = _F(ALPHA = 0.25,DELTA = 0.5,),
EXCIT = _F(CHARGE = clamp,FONC_MULT = castle,),
INCREMENT = _F(LIST_INST=time,),);
Here the standard parameters are given:
MODELE for the defined model, CHAM_MATER for the material properties, and since we use shell elements (coque_3d) also the CARA_ELEM is required. For the numerical integration we need the stiffness, mass and damping matrices MATR_RIGI, MATR_MASS and MATR_AMOR. The integration method is defined: in this case NEWMARK with default alpha and delta parameters. The excitation has been discussed previously: the structure clamp and the scaling function castle. Finally the integration time is defined in INCREMENT.
Although the damping matrix Mdampg has been defined here, in the first part the calculation will be performed without damping. See for more detailed discussion of damping matrix later on.
Results
Since we use a quad9 element (coque_3d), that cannot be displayed in Salome, we have to project the results to the quad8 mesh suitable for Salome and write the results to file.
SALmodes=PROJ_CHAMP(RESULTAT=Rdyn,
MODELE_1=modelc,
MODELE_2=modinit,);
IMPR_RESU(FORMAT='MED',
UNITE=21,
RESU=_F(MAILLAGE=meshinit,
RESULTAT=SALmodes,
NOM_CHAM='DEPL',),);
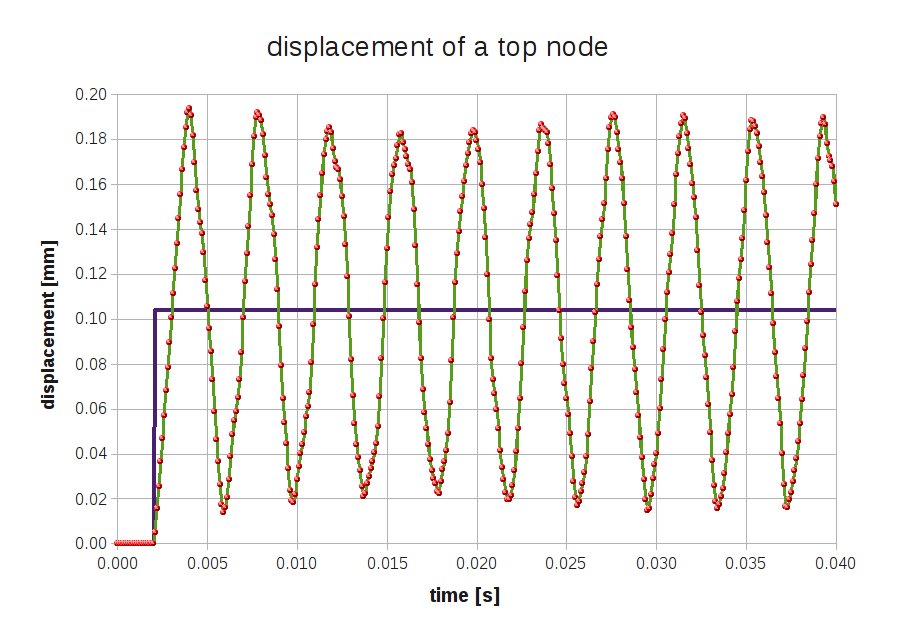
For reference, the static, axial displacement Uz according to 'beam theory' is Uz = FL/(EA) = 5500.0*5/(2.1E5*pi*dcyl*th) = 0.1042 mm.
Writing displacements of a single node
Since we would like to see the time response of the cylinder, we write the displacements of a single node (node Ntop) on top of the cylinder to file. This node has already defined in Salome and is part of the med file.
TB_nodf=POST_RELEVE_T(ACTION=(_F(OPERATION='EXTRACTION',
INTITULE='displacements',
RESULTAT=Rdyn,
NOM_CHAM='DEPL',
TOUT_ORDRE='OUI',
GROUP_NO='Ntop',
RESULTANTE=('DX','DY','DZ',),
MOYE_NOEUD='NON',),),
TITRE='Displacement top of cylinder',);
#Finally, write the data to a file (define a file in ASTK with file unit 26, in this case).
IMPR_TABLE(TABLE=TB_nodf,
FORMAT='TABLEAU',
UNITE=26,
SEPARATEUR=' * ',
TITRE='displacements at nodes on group Ntop',);
Note that in the POST_RELEVE_T command, the parameter RESULTANTE=('DX','DY','DZ',), could be replaced by RESULTANTE=('DZ',), because z is the only relevant displacement direction.
Axial mode shape
- Intermezzo
Now we determine the axial resonance frequency by a modal analysis. The interesting frequency range is given below:
NUMERO FREQUENCE (HZ) NORME D'ERREUR
:
19 2.51044E+02 3.35198E-13
20 2.51048E+02 1.35509E-12
21 2.54893E+02 1.37199E-13
22 2.66328E+02 4.59886E-11
23 2.66329E+02 3.96433E-12
:
Mode number 21 is the axial mode shape of the cylinder. Also, it is the first single modal frequency and therefore easy to distinguish. All other mode shape are double. These represent bending modes in both x and y direction.
Time domain response - no damping
The time response of a top node is given in the picture below. The resonance frequency nicely corresponds with the previously determined 255 Hz, ie. the time of a single sine wave is about 4 ms. Note that the system is undamped.
Applying viscous damping proportional to stiffness and mass matrices
In the previous section the damping matrix -although defined- is zero. Here we use viscous damping proportional to the stiffness and mass matrices, or Rayleigh damping. The differential equation to be solved is:
Ms2x Csx Kx = F(t
For Rayleigh damping, the viscous damping matrix is assumed to be
C = K M. K is the stiffness matrix, M is the mass matrix and the resulting damping matrix is C.
The main characteristics are:
- damping proportional to stiffness: zeta = (alpha_j/omega_j)*omega, ie higher frequencies are more damped
- damping proportional to mass: zeta = (beta_j*omega_j)/omega, ie lower frequencies are more damped
- a combination of both characteristics yields a bathtub curve with higher damping at low and high frequencies
- For more details see [R5.05.04, specially page 9/13].
Damping proportional to the stiffnes matrix
First we use a damping proportional tot the stiffness matrix: alpha = alpha_j and beta = 0. In the material definition we add the AMOR_ALPHA and AMOR_BETA parameters:
a_alpha = 5e-4 a_beta = 0.00 steel=DEFI_MATERIAU(ELAS=_F(E=2.100e5,NU=0.28,RHO=0.007850,AMOR_ALPHA=a_alpha,AMOR_BETA=a_beta,),);
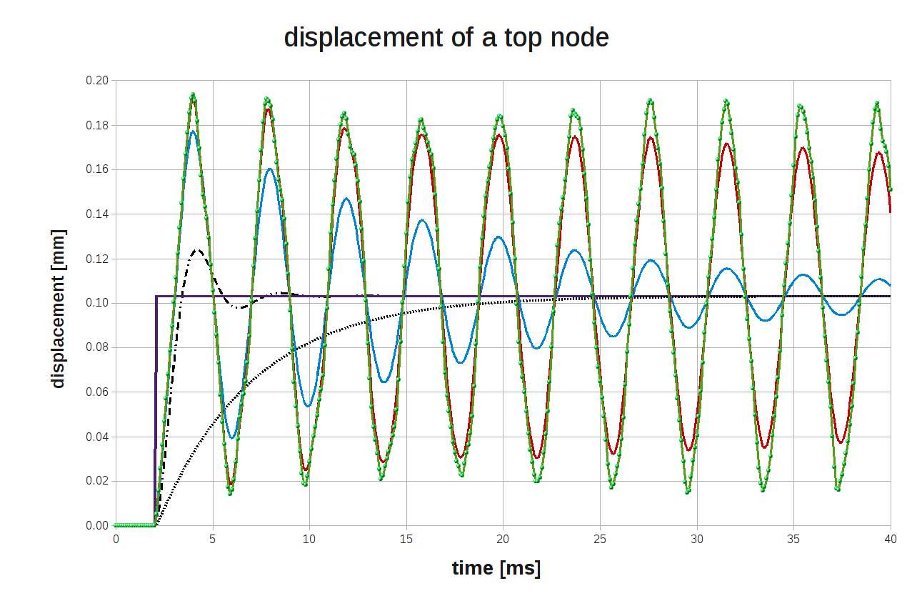
The radial frequency of the axial mode is about 1600 rad/s. In the picture below various values of AMOR_ALPHA have used: they range from 5e-3 to 5e-6.
green curve with dots: a_alpha = 0 [s]
red curve: a_alpha = 5e-6 [s]
blue curve: a_alpha = 5e-5 [s]
black curve: a_alpha = 5e-4 [s] *)
black dotted curve: a_alpha = 5e-3 [s]
Damping proportional to the mass matrix
For damping proportional to the mass matrix we set alpha to 0 and beta = beta_j.
a_alpha = 0.00 a_beta = 5e+1 steel=DEFI_MATERIAU(ELAS=_F(E=2.100e5,NU=0.28,RHO=0.007850,AMOR_ALPHA=a_alpha,AMOR_BETA=a_beta,),);
green curve with dots: a_beta = 0 [1/s]
red curve: a_beta = 50 [1/s]
light blue curve: a_beta = 500 [1/s]
dark blue curve: a_beta = 2000 [1/s] *)
black curve: a_beta = 5000 [1/s]
Note:
- the different time scale
- the lower damping at higher frequencies for damping proportional to the mass matrix
Rayleigh damping - alpha and beta
For both alpha and beta unequal to zero we have damping proportional to the stiffness and mass matrix. In this case we choose alpha equal to alpha0 = 5e-5 [s] and after some iterations we find that for more or less equal damping beta is equal to beta0 = 130 [1/s]. We just compare the results in time domain during 5 cycles. Then halving both values we obtain a general Rayleigh damping with alpha and beta equal to alpha0/2 and beta0/2. The results are shown in the next picture.
red curve: 'stiffness' damping - alpha = alpha0 = 5e-5 [s] - beta = 0
green curve: 'mass' damping - alpha = 0 - beta = beta0 = 130 [1/s]
blue curve: Rayleigh damping - alpha =alpha0/2 - beta = beta0/2
Remark - personal note ....
(*) The frequency of the resonance mode is 255 Hz or 1600 rad/s. The dark blue curve obtained for a_beta = 2000 roughly corresponds to this value. This value is also close to the critical value of the damping coefficient. So as a first guess for critical damping put beta equal to the (interesting) resonance frequency in [rad/s]. Using the same reasoning for damping proportional to stiffness: for critical damping put a_alpha equal to 1/omega_o (6e-4 s/rad). .......
And for reference see e.g. [Rayleigh Damping - note the changed definition of alpha and beta in this publication!].
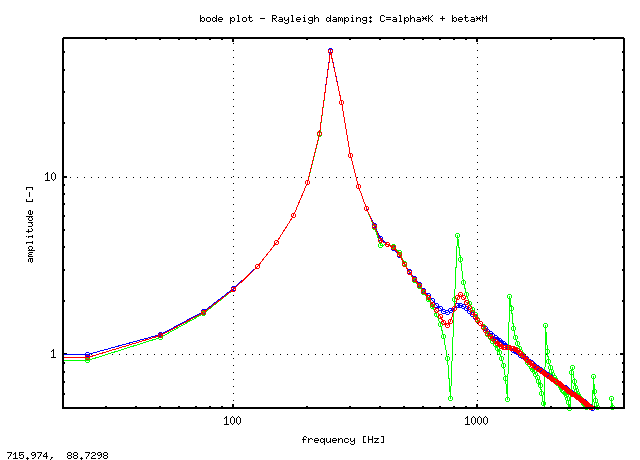
The bode plot for Rayleigh damping
In the bode plot, determined by Octave from the same time series as the graph above, the frequency domain characteristics are readily visible.
green curve: alpha = 0 and beta = beta0 - mass damping - higher frequency hardly damped
red curve: alpha = alpha0/2 and beta = beta0/2 moderate damping over frequency range
blue curve: alpha = alpha0 and beta = 0 - stiffness damping - higher frequency too much damped
Note that alpha0 and beta0 have been chosen such that the resonance at 255 Hz is about the same for 'mass' damping, 'stiffness' damping and the combined case.
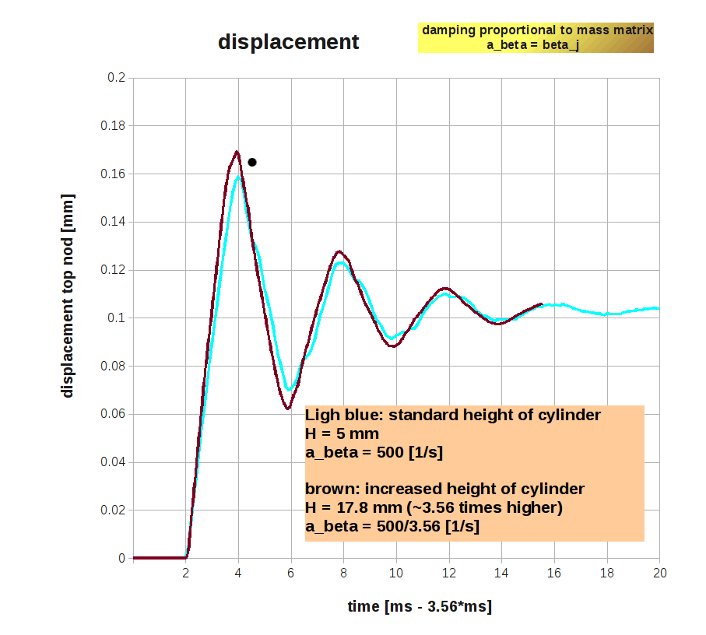
Influence of resonance frequency on 'mass' damping
To verify the influence of the resonance frequency the height of the cylinder has been changed by a scaling factor of 3.56. The axial resonance frequency -inversely proportional to the height of the cylinder- changes by the same amount; from 255 Hz to 72 Hz. Then in order to obtain the same damping coefficient the parameter a_beta changes from e.g. 500 [1/s] to 500/3.56 [1/s]. In the graph below the behaviour of the standard and enlarged cylinders are given. The displacement and time axis have been scaled accordingly.
For the brown curve, increased cylinder:
- time scaled by 3.56
- displacements scaled by 2.88 (apparently the boundary conditions influence the axial displacements).
This is for now my interpretation of alpha and beta. Maybe the documentation gives more information, so please add relevant parts here ......
Download files
This zip contains the following files
- python geometry and mesh files (load in Salome by File --> Load script (cntrl T)) and right select refresh (F5) in the object browser). Export the med file in the mesh module under cylinder.med for further processing by Code-Aster, controlled by ASTK.
- command files for Code-Aster:
- - modal.comm, modal analysis for testing axial frequencies
- - dynload.comm, dynamic analysis of the structure due to axial load. If you are unhappy with the comm files, please modify them with the command file editor Eficas (Tools menu in ASTK).
- astk file for file control by ASTK
- table.txt, text file with nodal displacements for each time step of a top node (N137).
The result file dyn2res.med can be viewed in the post processor module of Salome by File --> Import --> dyn2res.med or cntrl I in the object browser.
Note on Code Aster 10:
Code Aster 10+ is stricter then CA9- with respect to the MODI_MAILLAGE keyword in CREA_MAILLAGE. In case no TRIA6 or QUAD8 elements are available in the mesh, change near line 30 in both command files:
meshmod=CREA_MAILLAGE(MAILLAGE=meshinit,
MODI_MAILLE=(_F(TOUT='OUI',OPTION='QUAD8_9',),
_F(TOUT='OUI',OPTION='TRIA6_7',),),);
to, for QUAD8 mesh only:
meshmod=CREA_MAILLAGE(MAILLAGE=meshinit,
MODI_MAILLE=(_F(TOUT='OUI',OPTION='QUAD8_9',),),);
or, for TRIA6 mesh only:
meshmod=CREA_MAILLAGE(MAILLAGE=meshinit,
MODI_MAILLE=(_F(TOUT='OUI',OPTION='TRIA6_7',),),);
References
[R5.05.04] Modélisation de l'amortissement en dynamique linéaire
[U2.06.03] Notice de modélisation de l'amortissement mécanique
[U4.61.01] Opérateur CALC_MATR_ELEM
[U4.43.01] Opérateur DEFI_MATERIAU
[R5.06.01] Réduction de modèle en dynamique linéaire et non-
linéaire : Méthode de RITZ
[R5.06.04] Algorithmes d’intégration temporelle de l’opérateur DYNA_TRAN_MODAL
[Rayleigh Damping] Computation of Rayleigh Damping Coefficients for Large Systems, by Indrajit Chowdhury and Shambhu P. Dasgupta.
[Note that alpha and beta have been interchanged here compared to Code Aster definition!]
that is all for now
september 2009
kees wouters