Contrib:KeesWouters/beambuckling
Contents
Buckling behaviour of a beam
To start with, this contribution mainly focuses on the use of Salome and Code Aster, not on the results and the mechanical justifications of the code that has been used. So no garantees that the results will be correct upto the fifth decimal place, which they are not. I do hope though that this information is useful. For me it has been, because I had to think about some commands and look through the documentation and learn from that. In case of mistakes, errors and the like, please notify me, or better, you are invited to correct them yourself. Enjoy.
General discription of the calculation
First the geometry is defined in Salome. The mechanical properties and loads are defined in the C-Aster command file. In order to determine the geometrical stiffness matrix, a linear calculation is carried out and the corresponding stresses in the construction are determined.
The stiffness matrix is available from the linear case and can be extracted. The geometrical stiffness matrix can be derived from the calculated stresses in the construction. Finally an eigenvalue analysis is then carried out to determine the buckling load.
At the end the files defining the geometry and mesh in Salome, the command file and astk file for Code Aster can be downloaded.
Critical load according to Euler
The construction is a prismatic beam with diameter 1 and length 50 mm. The material is steel. According to Euler the the critical load with fixed i.e clamped boundary conditions at both ends of the beam is
- Fcr = E*Iss*(pi/(k*L))^2,
- k = 0.5 for clamped boundary conditions
- Youngs' modulus E = 2.1e5 MPa
- poisson ratio nu = 0.28, not needed for the Euler beam
- smallest moment of inertia Iss = pi/64*d^4 = 0.049 mm4
- length of the beam L = 50 mm
- corresponding axial load Fax = Cz*Uz = EA/L * Uz = 3298.7 * 0.2 = 659.7 N
- Fcr = 162.8 N or a ratio of
- ratio = Fcr/Fax = 0.247
This last value is what we are looking for in the buckling analysis with Code-Aster.
Defining the properties of the beam
Geometry of the beam
The construction is readily defined in the Geometry module of Salome by Cylinder, radius 0.5 and length 50 mm, at the origin of the coordinate system. The axial direction of the beam coincides with the global z axis. The two axial faces of the beam are denoted by 'bot' and 'top', used to apply boundary conditions and loads.
Beam with solid elements
The mesh is generated by NetGen. The choosen algorithm is tetrahedron (NetGen), NetGen 1D 2D 3D. The applied hypothysis are: Maximum volume 0.25, maximum size 0.125. Second order elements are generated, finess is moderate, and optimize is set. A face group is generated for top and bot. The boundary conditions will be dx=dy=dz=0 at the 'bot' and dx=dy=0, dz=-0.2 mm at 'top', see command file for this further on.
Material properties of the beam
The beam consists of steel. The material properties are as given above.
Result of Code-Aster
Linear load case for determining the stresses
First the linear load case has to be solved to determine the stresses in each element. Use the commands:
- result=MECA_STATIQUE(MODELE=pmodel,CHAM_MATER=matprops,EXCIT=(_F(CHARGE=FLoad,),),);
- result=CALC_ELEM(reuse=result, ...);
- result=CALC_NO(reuse =result, ...);
- IMPR_RESU(FORMAT='MED',...,RESU=_F(MAILLAGE=pmesh,RESULTAT=result,..,),);
In order to verify the calculation we determine the force on the top plane. Since we applied a displacement on the top, we are interested in the corresponding axial force. On this plane, the extracted axial force is -660.4 N, slightly more than the analytic result.
The nodal forces, reaction forces and displacements of the top plane can be extracted from the result by defining a table and write them to a file:
- pmesh=DEFI_GROUP(reuse=pmesh,MAILLAGE=pmesh,CREA_GROUP_NO=_F(NOM='top',GROUP_MA='top',),);
- TB_nodf=POST_RELEVE_T(ACTION=
- _F(OPERATION='EXTRACTION',..,NOM_CHAM='DEPL',..,GROUP_NO='top',..),
- _F(OPERATION='EXTRACTION',..,NOM_CHAM='FORC_NODA',..,GROUP_NO='top',.),..);
- IMPR_TABLE(TABLE=TB_nodf,FORMAT='TABLEAU',UNITE=26,SEPARATEUR=' * ', ...);
The content of the file, again defined in ASTK:
#displacements at nodes on group TOP #[Reaction] Nodal Forces * INTITULE * RESU * NOM_CHAM * NUME_ORDRE * INST * DX * DY * DZ * displacements * result * DEPL * 1 * 0.00000E+00 * -7.30250E-19 * -3.47836E-17 * -4.08000E+01 * NodalForces * result * FORC_NODA * 1 * 0.00000E+00 * 2.83321E-06 * 8.20372E-06 * -6.60449E+02
The nodal forces are the sum of the forces acting on each node.
Note the the displacements DX, DY and DZ are the sum of 204 nodes on the top plane, ie. DZ = -0.2*204 = -40.8 mm.
So the given displacement depends on the fineness of the mesh.
Element stiffness matrix and geometrical stiffness matrix
In order to determine the buckling load of a construction, the element stiffness matrix and the geometrical stiffness matrix need to be known. The element stiffness is in principle available from the linear case. The geometrical stiffness matrix depends on the stress internal in the construction, depending on the load case. Hence the stress needs to be extracted from the linear load case. Then the geometrical stiffness matrix can be determined.
Depending on the boundary conditions and maybe other relations, these stiffness matrices need to be ordered in the correct way before an eigenvalue extraction can be applied. Therefore both matrices need to be ordered according to the numbering of the degrees of freedom, dof or ddl.
We need to:
- determine stiffness matrix Smech
- determine stress field in the elements Fsigma
- determine geometrical stiffness matrix Sgeom
- determine order for degree of freedom nddl
- determine newly ordered stiffness matrix SAmech
- determine newly ordered geometrical stiffness matrix SAgeom
The following C-Aster commands are used to do just this:
- Smech = CALC_MATR_ELEM(OPTION='RIGI_MECA',MODELE = pmodel,CHARGE = FLoad, CHAM_MATER = matprops,);
- Fsigma = CREA_CHAMP(OPERATION='EXTR',TYPE_CHAM='ELGA_SIEF_R',RESULTAT=result,NUME_ORDRE=1,NOM_CHAM='SIEF_ELGA_DEPL',);
- Sgeom = CALC_MATR_ELEM(OPTION='RIGI_GEOM',MODELE=pmodel,SIEF_ELGA=Fsigma,);
- nddl = NUME_DDL(MATR_RIGI=Smech);
- SAmech = ASSE_MATRICE(NUME_DDL=nddl,MATR_ELEM=Smech,);
- SAgeom = ASSE_MATRICE(NUME_DDL=nddl,MATR_ELEM=Sgeom,);
The last two matrices SAmech and SAgeom can be used in an eigenvalue analysis.
Eigenvalue extraction by Sorensen iteration
The following eigenvalue problem, with the previously defined stiffness matrices SAmech and SAgeom need to be solved:
- (SAmech + mu*SAgeom)x = 0 or SAmech*x = *SAgeom*x [mu = -]
In the C-Aster eigenvalue codes the last form is used, so afterwards we need to change the sign of the eigenvalue. In most cases the best choice to use Sorensen for extracting eigenvalues. To calculate and save the results in a file the following two commands are used:
# multiply eigenvalues by -1 or reverse force, since we solve
# A*x = lamdba*B*x iso (A+mu*B)x=0
buckle = MODE_ITER_SIMULT(INFO=1,
MATR_A = SAmech,
MATR_B = SAgeom,
METHODE = 'SORENSEN',
PREC_SOREN=2e-16,
NMAX_ITER_SOREN=50,
TYPE_RESU= 'MODE_FLAMB',
CALC_FREQ = _F(OPTION = 'PLUS_PETITE',NMAX_FREQ=6,),);
IMPR_RESU(FORMAT='MED',
UNITE=21,
RESU=_F(MAILLAGE=pmesh,
RESULTAT=buckle,
NOM_CHAM='DEPL',),);
In the mess file the following critical loads charge critique are found, six eigenvalues are requested:
CALCUL MODAL: METHODE D'ITERATION SIMULTANEE
METHODE DE SORENSEN
NUMERO CHARGE CRITIQUE NORME D'ERREUR 1 -9.72998E-01 3.68322E-09 2 -9.72990E-01 3.42967E-09 3 -5.00953E-01 5.82225E-09 4 -5.00949E-01 6.01805E-09 5 -2.45979E-01 3.26885E-08 6 -2.45977E-01 3.10062E-08 NORME D'ERREUR MOYENNE: 0.13775E-07
Some remarks:
- - for buckling analysis use TYPE_RESU=‘MODE_FLAMB’; use TYPE_RESU=‘DYNAMIQUE’ for modal analysis
- - do not search for only one eigenvalue NMAX_FREQ=1 because this causes the calculations to take a very long time. (Since the Sorenson method is basicly a subspace method, it needs more eigenvectors to track the eigenvalues properly ...??)
- - the machine precision can be omitted (PREC_SOREN=2e-16)
- - the default number of iterations is NMAX_ITER_SOREN=20, I increased this to 50. Though in most cases 20 is alright.
The bold values of modes 5 and 6 nicely correspond with the analytic values 0.247 found earlier. Note:
- The way C-Aster calculates the eigenvalue problem causes a change of sign for the eigenvalue (see references at the end).
- Modes 5 and 6 are the lowest eigenvalues of the total extracted 6 values. These are of course the critical values of the buckling analysis.
- Modes 5 and 6 (and 3 - 4 and 1 - 2) are the same shapes in the x and y directions.
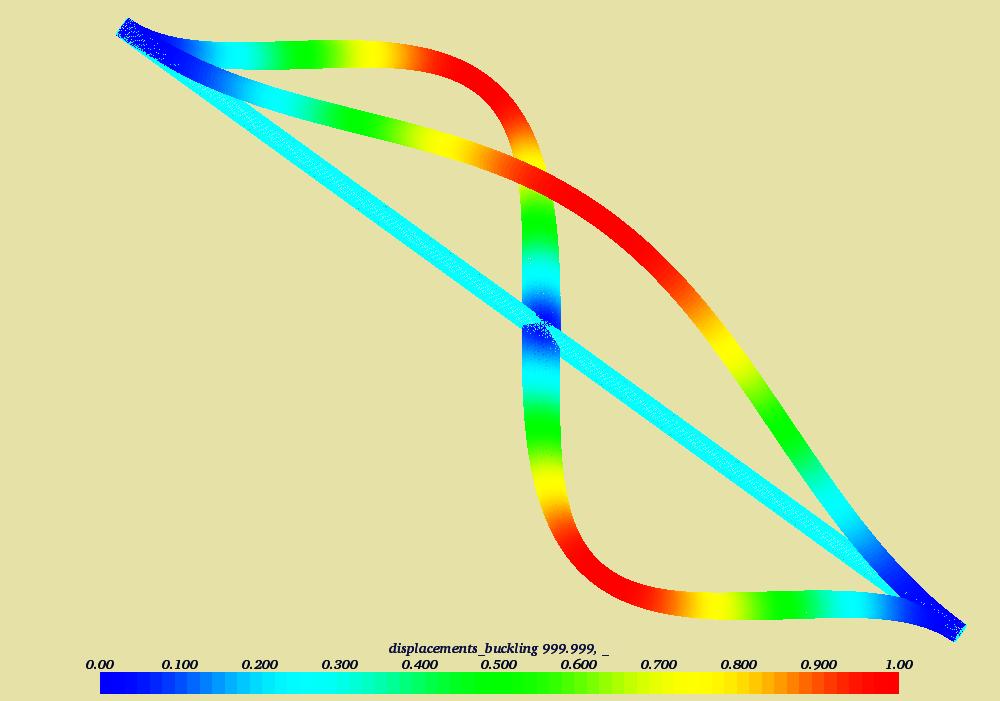
Buckling modes 1 and 2
As usual, a picture to finalise the calculation. The first and second buckling mode are given in the picture.
The first mode (halve sine wave) the depicted one is in x direction, whereas the second mode (full sine wave) is in y direction.
Only the first mode is relevant.
Buckling modes of v-shaped beam
Geometry and load of the v-shaped beam
the geometry is taken from [here].
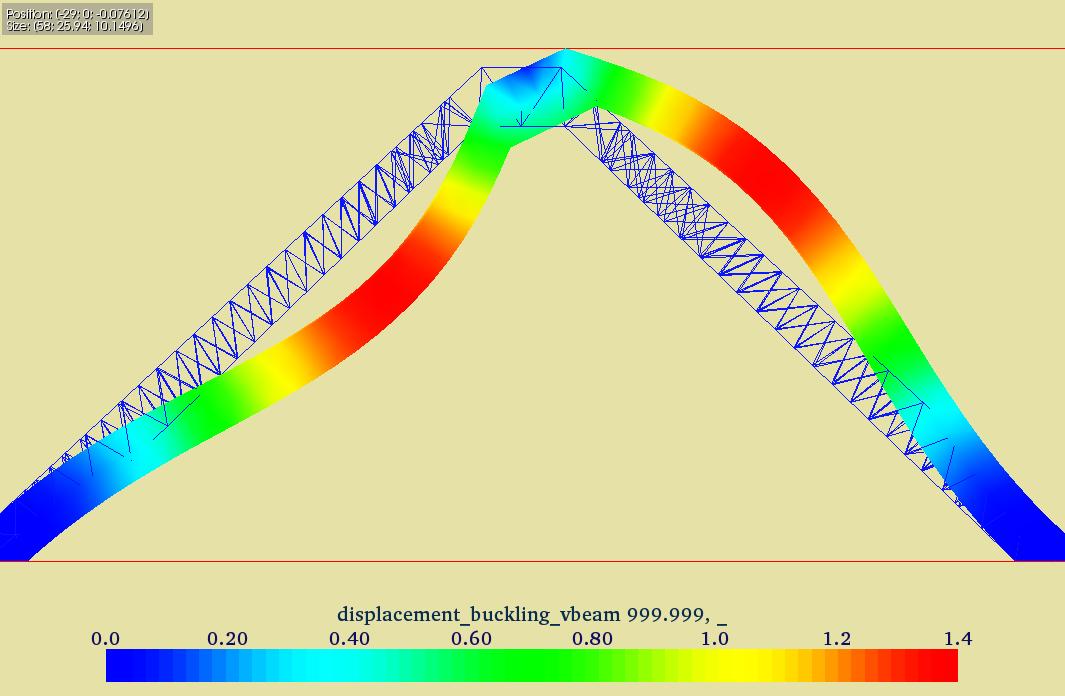
Here the first buckling mode of v-shaped beam is presented.
The calculation is the same as described above. The applied load is a pressure on the top face (Pforce has been renamed top; whereas Pleft, Prigth has been joined together to fix for this case.)
pressure = pressure = 1000.0 #note: area of 'top' is 4*10 = 40 mm2
FLoad=AFFE_CHAR_MECA(MODELE=pmodel,
DDL_IMPO = (_F(GROUP_MA='bot',DX=0.0,DY=0.0,DZ=0.0,),),
PRES_REP = (_F(GROUP_MA='top',PRES=pressure,),),);
The normal vector on the top face can be depicted in Salome by right click in the viewer window on the construction and select Orientation of Faces. Depending whether a linear or quadratic mesh has been choosen, you get the following view:
You can easily change between linear and quadratic elements by Modification --> convert to/from quadratic in the mesh module.
Note that for a linear mesh, each element face has one normal vector at the center. For the quadratic mesh the normal vectors are more 'randomly' distributed.
First buckling mode
Applying a total pressure of 1000.0 Pa on the top face yields an eigenvalue of -1.23704. Hence the buckling load is -1237 Pa, or -49.5 kN (area is 40 square mm).
References
- Opérateur MODE_ITER_SIMULT: http://www.code-aster.org/V2/doc/v9/man_u/u4/u4.52.03.pdf
- Opérateur MODE_ITER_INV: http://www.code-aster.org/V2/doc/v9/man_u/u4/u4.52.04.pdf
- Opérateur MACRO_MATR_ASSE: http://www.code-aster.org/DOCASTER/Man_U/U4/U46121g1.pdf
- Opérateur ASSE_MATRICE: http://www.code-aster.org/DOCASTER/Man_U/U4/U46122h.pdf
- Opérateur NUME_DDL: http://www.code-aster.org/V2/doc/v9/man_u/u4/u4.61.11.pdf
MODE_ITER_SIMULT, paragraph 3.1:
La recherche de mode de flambement linéaire. Dans le cadre de la
théorie linéarisée, en supposant a priori que les phénomènes de stabilité sont
convenablement décrits par le système d'équations obtenu en supposant la
dépendance linéaire du déplacement par rapport au niveau de charge critique,
la recherche du mode de flambement x associé à ce niveau de charge critique
mu = -, se ramène à un problème généralisé aux valeurs propres de la forme
- (Kmu*Kg*x=0 ⇔ K*x =Kg*x
- K = A, (stiffness matrix)
- Kg = B, (geometrical stiffness matrix)
K matrice de rigidité matérielle et Kg matrice de rigidité géométrique. Les modes avec propres manipulés (l,x) sont à valeurs réelles. Ce type de
problématique est activé par le mot-clé TYPE_RESU='FLAMBEMENT' et génère une
structure de données Aster de type mode_flamb.
Attention:
• Dans le code, on ne traite que les valeurs propres du problème
généralisé, les . Pour obtenir les véritables charges critiques, les mu, il
faut les multiplier par –1.
• En GEP, pour traiter des problèmes à modes complexes (matrices non
symétriques et/ou à valeurs complexes), il faut utiliser
MODE_ITER_SIMULT ('METHODE='SORENSEN'/'QZ').
Download files
This zip contains the following files
- python geometry and mesh files (load in Salome by File --> Load script (cntrl T)) and right select refresh (F5) in the object browser)
- command file for Code-Aster
- astk file for file control of ASTK
- text file with nodal displacements and force on plane top
The result file buck2res.med can be viewed in the post processor module of Salome by File --> Import --> buck2res.med or cntrl I in the object browser.
The same file types for the v-shape beam: