Contrib:KeesWouters/bc/pythonlist
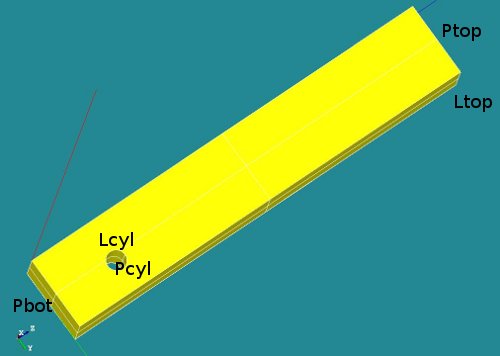
Geometry and mesh of the block with cylindrical hole
Applied on a simple block with a cylindrical hole the use of LIAISON_DLL is shown to simulate a cylindrical coordinate system
Contrib:KeesWouters/bc/cylinder
Geometry and mesh of the block with cylindrical hole
- key words
o LIAISON_DDL
o simulated cylinder coordinates and boundary conditions
Contrib:KeesWouters/bc/pythonlist
Rotation axis defined by Python list
- key words
o LIAISON_DDL
o simulated cylinder coordinates and boundary conditions
o Python list for applying boundary conditions
Contents
- 1 Geometry and mesh of the block with cylindrical hole
- 2 Material properties of the block
- 3 The cylindrical boundary conditions
- 4 The boundary conditions applied to the block
- 5 Command file for Code-Aster v11
- 6 The results of the calculation
- 7 Hinge defined by RBE3 constrained
- 8 Input files for the FE Analysis
- 9 References
- 10 Input files for the FE Analysis and references
Geometry and mesh of the block with cylindrical hole
This construction shows the use of LIAISON_DDL to simulate boundary condition on a cylindrical hole. It just shows the use of it.
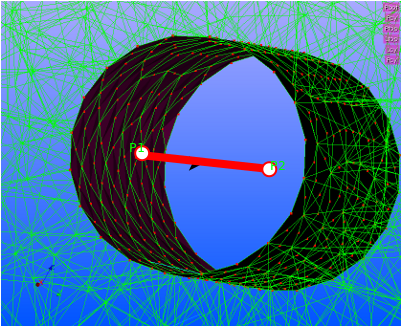
The boundary conditions ore build around a cylindrical hole in a block. The nodes attached to the cylinder are restricted to rotate around its central axis. The definition of this axis is done by two points P1 and P2 that need to be provided.
The geometry consists of a block with a cylindrical hole near the bottom side. The overall dimensions of the block are [Lx * Ly * Lz] = [2.0 * 3.5 * 20.0 ]. The hole is placed on the x-plane at position [yc, zc] = [2.0, 3.0]. The radius of the hole is R=0.45.
Some images of the construction:
A number of groups has been defined (P for plane, L for line segments):
- Ptop (not used)
- Pbot (not used)
- Pcyl (could be used to define nodes on this surface)
- Lcyl (not used in final version) and
- Ltop, used to apply boundary conditions in x and y direction.
Material properties of the block
The material property of the block is set to steel.
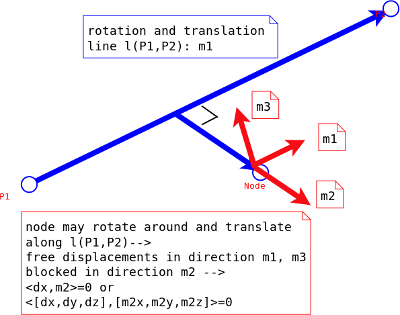
The cylindrical boundary conditions
Below an image to illustrate how to restrict these degrees of freedom:
In vector notation or Numpy - Python notation :
m1 = p2-p1 ## rotation axis m2 = Node-p1 ## m2* in the picture m3 = cross(m2,m1) ## Node may not be on rotation axis--> m2=a*m1 -->m3=0 m2 = cross(m1,m3) ## normal vector from line(P1,P2) to Node lm2 = sqrt(dot(m2,m2)) ## length of m2 m2 /=lm2 ## normalise m2 to unit vector
The two points P1 and P2 define the rotation axis (and, but not neccessarely, the cylinder). The nodes on the cylinder area may move freely in the direction of the vectors m1 and m3. In the direction of vector m2, normal to the rotation axis, the displacement is restricted. This restriction may be described by setting the inner or dot product of the dispacement vector dX = [dx, dy, dz] and the normal vector m2 = [m2x, m2y, m2z] to 0:
<dX, m2> = <[dx, dy, dz], [m2x, m2y, m2z]> = 0.
This is exactly the restriction that can be described by the C-Aster command LIAISON_DDL:
LIAISON_DDL=(_F(NOEUD=('Ni','Ni','Ni'),DDL=('DX','DY','DZ'),COEF_MULT=(alpha1,alpha2,alpha3),COEF_IMPO=beta) or
LIAISON_DDL=(_F(NOEUD=('Ni','Ni','Ni'),DDL=('DX','DY','DZ'),COEF_MULT=(m2x,m2y,m2z),COEF_IMPO=0)
where 'Ni' is a node number located on the cylinder area, eg, 'N123'. This command has to be implemented for every node on the cylinder, so we use Python to make this a bit easier and faster.
Remember that the part in the _F(...) operator can be placed in a Python list, dictionary, or tuple, eg:
_F(NOEUD=('N17', 'N17', 'N17'),DDL=('DX', 'DY', 'DZ'),COEF_MULT=(0.0, -0.588, 0.809),COEF_IMPO=0.0,),)
is the same as, or equivalent to:
{'NOEUD'=('N17', 'N17', 'N17'),DDL=('DX', 'DY', 'DZ'),'COEF_MULT'=(0.0, -0.588, 0.809),'COEF_IMPO'=0.0,)}
So in the Python script we iterate over all nodes on the cylinder area 'Ncyl' and append
bc.append({'NOEUD'=('N17', 'N17', 'N17'),DDL=('DX', 'DY', 'DZ'),'COEF_MULT'=(0.0, -0.588, 0.809),'COEF_IMPO'=0.0,})
this sequence for all selected nodes.
Remark:
The general format of the LAISON_DDL argument is:
_F(NOEUD=('Ni','Nj',....,'Nk'),
DDL=('DX','DY,......,'DRZ'),
COEF_MULT=(alphai,alphaj,....,alphak),
COEF_IMPO=beta)
where 'Ni' can be any selection of nodes
'DX','DY',...,'DRZ', can be 'DX','DY','DZ','DRX','DRY','DRZ', and probably other degrees of freedom offered by the current analysis.
alphai are the coefficients to the corresponding node degree of freedom of node 'Ni' and
beta is the right hand side
alphai*DX(Ni) + alphaj*DY(Nj) + ..... + alphak*DRZ(Nk) = beta
Of course, the number of arguments in NOUED, DDL and COEFF_MULT must be equal for one sequence. They may differ between various sequences however.
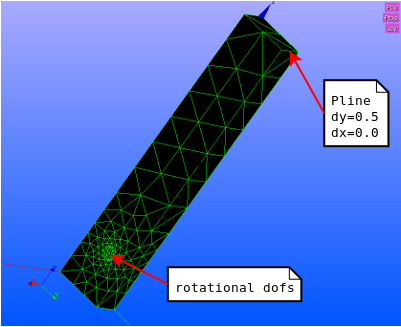
In the picture below you see the cylinder and other boundary conditions on the block.
Python code for list for free rotation
Since we are going to use mesh information in the Python script language, we need to define:
DEBUT(PAR_LOT='NON')
We will also need some modules defined in the ...Utilitai.partition folder:
from Utilitai.partition import * import sys import numpy
need_MAIL_PY_help=False ## obvious other choise is True if need_MAIL_PY_help: from Utilitai.partition import * help(MAIL_PY)
PyMesh = MAIL_PY() ## convert CodeAster mesh to Python PyMesh.FromAster(mesh); nonu = PyMesh.dime_maillage[0] ## number of nodes elnu = PyMesh.dime_maillage[2] ## number of elements test=CmeshCA.dime_maillage[5] ## [min,max] dimension: [0,5] NodeCoord = PyMesh.cn ## xyz coordinates of nodes (nonu*3 matrix) ElemConnect = PyMesh.co ## node numbers of elements (elnu*x matrix) NodeList = list(PyMesh.correspondance_noeuds) ElemList = list(PyMesh.correspondance_mailles) ElemType = list(PyMesh.tm) NodeGroup = PyMesh.gno ## list of GROUP_NO groups (see help(MAIL_PY) for object methods reference) ElemGroup = PyMesh.gma ## list of GROUP_MA groups, eg groupstr
This part of the script extracts the nodes and coordinates of the cylinder area that need to have the rotational degrees of freedom. Note that the group of nodes has already been defined in Salome and is called 'Ncyl'.
NodeCount = 0
groupstr = 'Ncyl'
ddl_condition=[] ## initialise ddl_condition list
for ii in xrange(len(NodeGroup[groupstr])):
NodeNumber = NodeGroup[groupstr][ii]
#print 'NodeGroup: ',ii,NodeNumber,NodeCount
NodeCount+=1
NNxyz = NodeCoord[NodeNumber]
nx,ny,nz = cylinder_normal(P1,P2,NNxyz)
NodeCount+=1
NNp1 = NodeNumber+1 # node numbers are increased by 1: Salome <--> Code Aster
ddl_condition.append({'NOEUD': ['N%d'%(NNp1),'N%d'%(NNp1),'N%d'%(NNp1)], 'DDL':['DX','DY','DZ'], 'COEF_MULT': [nx,ny,nz],'COEF_IMPO':0.00})
if info>1:
#print {'NOEUD': ['N%d'%(NNp1),'N%d'%(NNp1),'N%d'%(NNp1)], 'DDL':['DX','DY','DZ'], 'COEF_MULT': [nx,ny,nz],'COEF_IMPO':0.00}
print ddl_condition[ii]
if info>0:
# check format of bc_list
print ic,countntop,': ',ddl_condition[0]
print '::::::::::::::::::::::::::'
print ic,countntop,': ',ddl_condition[-1]
Now the list can be used in the AFFE_CHAR_MECA command just as the _F(...) operator:
rotcyl=AFFE_CHAR_MECA(MODELE=Cmod,LIAISON_DDL = ddl_condition);
This part may be implented as a Python file, see the chapter for C-Aster version11.
The boundary conditions applied to the block
- On the top line segment Ltop a non zero displacement in y direction is prescribed. The displacement in z direction is fixed.
- On the nodes connected to the cylindrical hole a tangential displacement is allowed. The radial component is fixed. The displacement in axial or x direction is free. Due to this restriction the displacement of the geometry in z direction is defined.
We apply a displacement on a line of the top plane in y direction DY=0.5 and keep it fixed in x direction: DX=0:
- The boundary condition on the line segment Ltop:
- bcforce=AFFE_CHAR_MECA(MODELE=Cmod,DDL_IMPO=(_F(GROUP_MA='Ltop',DY=0.5,DX=0.0000),),);
Then we apply the cylindrical boundary conditions to the node on the cylinder and let it freely rotate around the cylinder axis:
- The cylindrical boundary condition on the nodes of the cylindrical hole are defined by the LIAISON_DDL keyword in stead of DDL_IMPO:
- ... LIAISON_DDL=(_F(NOEUD=('Ni','Ni','Ni'),DDL=('DX','DY','DZ'),COEF_MULT=(alpha1,alpha2,alpha3),COEF_IMPO=beta),
Alright, just this took me several days to find out. But once you know, it is easy.
Command file for Code-Aster v11
updated january 2013
Code-Aster evolves, so a lot of commands have changed since v9-10 of Code Aster. The input files for v11 reflect these changes as well as some node selection.
Since we have to import a few Python files to define the rotation, in DEBUT we need to advice Code-Aster to talk to Python in an proper way:
DEBUT(PAR_LOT='NON');
import sys
sys.path.append("/cae_sg500/caexample/caelinux/csys1/python2a") ## define your own path here for import RotationAxisBC
from CA_geometry import RotationAxisBC
import numpy
The selection of nodes on the cylinder is now included in the command file:
Cmesh=LIRE_MAILLAGE(UNITE=20,FORMAT='MED',);
Cmesh=DEFI_GROUP(reuse =Cmesh,
MAILLAGE=Cmesh,
CREA_GROUP_NO=_F(NOM='Ncyl',GROUP_MA='Pcyl',),);
The geometry group Pcyl [GROUP_MA='Pcyl'] need to be defined in the mesh file. This is easy in eg Salome. The selection of the node group GROUP_NO='Ncyl', previously done in Salome, is now carried out by the DEFI_GROUP command (which I find easier).
Now returning to the definition of the free rotation of a cylinder around its axis: two points P1 and P2 define the centre line of the rotation axis (which may coincide with the centre axis of a cylinder). Ideally, these two point would be based on the selection of nodes, but so far I have figured out how to do that relatively easy.
Anyway, the points P1 and P1 are numpy arrays and define the rotation axis. The Python function RotationAxisBC(...) has five arguments:
- mesh: Cmesh
- group of nodes GROUP_NO 'Ncyl' that are restriction to rotate around the given axis
- two points: numpy arrays, P1 and P2 defining the rotation axis and
- info: [0|1|2] for printing controle
P1 = numpy.array([0.0, 2.0, 3.0]) P2 = numpy.array([2.0, 2.0, 3.0]) info = 0 ddl_condition = RotationAxisBC(Cmesh,'Ncyl',P1,P2,info) rotcyl = AFFE_CHAR_MECA(MODELE=Cmod,LIAISON_DDL=ddl_condition);
The result is a Python list ddl_condition that contains the previously derived part of LIAISON_DDL for all the nodes contained in the selection 'Ncyl'.
As always, the hard work is being done by the Python function RotationAxisBC(...).
More on this later ..., see for now the download files.
Finally, the list is applied to the MECA_STATIQUE command.
result=MECA_STATIQUE(MODELE=Cmod,
CHAM_MATER=Amat,
EXCIT=(_F(CHARGE=bcforce,),
_F(CHARGE=rotcyl),),);
Here the rotation axis and nodes on the cylinder area are shown.
[Note that the commands CALC_ELEM(...) and CALC_NODE(...) are not available in CA version 11+ anymore, see POST_CHAMP]
The results of the calculation
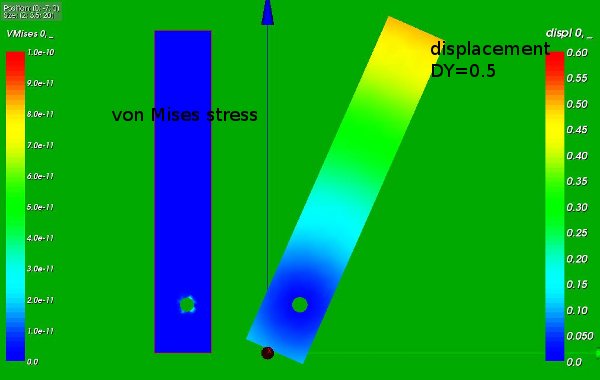
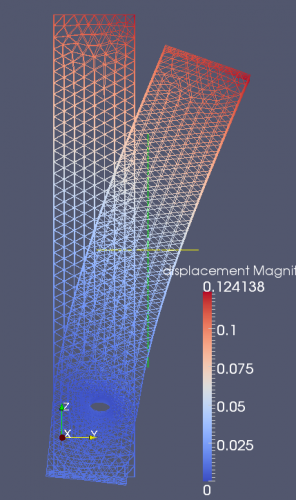
The following picture shows the rotation of the block around the cylindrical hole as well as the von Mises stress:
- The left part of the picture displays the von Mises stresses in the construction: they are zero to the working precision as we expect. The rotation around the cylinder is controlled by the displacement at the top edge and can be performed by a rigid body movement.
- The right part shows the displacement in y direction: the construction nicely rotates around the cylindrical hole.
Boundary conditions of top line: DX=0.5 and DY=0.0.
Changing the boundary conditions on the top plane shows that the boundary conditions on the cylinder also allow a slider function in the direction of the axis. The picture on the left hand side shows a displacement of 0.5 in x direction. The picture on the right hand side shows that the slider effect is stressless.
A bit of fooling around ...
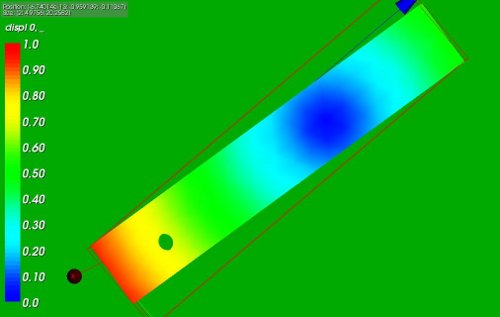
Selecting the same nodes around the cylindrical hole but choosing the rotating axis with an offset of 10 in z direction yields the following displacement:
*
This is easily performed by changing the two points P1 and P2:
Original coordinates, indicating the centre axis of the cylinder:
P1 = numpy.array([0.0, 2.0, 3.0]) P2 = numpy.array([2.0, 2.0, 3.0])
and change them to:
P1 = numpy.array([0.0, 2.0, 3.0+10.0]) P2 = numpy.array([2.0, 2.0, 3.0+10.0])
see also command file below.
Hinge defined by RBE3 constrained
[this part is still under construction]
In Code Aster the RBE3 connection is available. This can be used to define a hinge relatively easy. By connecting a master node Nmaster with any surface area by the RBE3 constrained and restricting the master node to have a single rotation only the hinge connection is established.
The relevant commands
The following C-Aster commands may be used to define the hinge.
First define the model for a discrete node, that may be added into the mesh on the axis of rotation:
CylModel=AFFE_MODELE(MAILLAGE=Cmesh,
AFFE=(_F(TOUT='OUI',
PHENOMENE='MECANIQUE',
MODELISATION='3D',),
_F(GROUP_NO='Nmaster',
PHENOMENE='MECANIQUE',
MODELISATION='DIS_TR',),),);
In order to create 6DOFs for the master node Nmaster a stiffness and mass is assigned to the node (with effective zero stiffness and mass):
N_stmass=AFFE_CARA_ELEM(MODELE=CylModel,
INFO=1,
DISCRET=(_F(CARA='M_TR_D_N',
GROUP_NO='Nmaster',
VALE=[1,0.0,0.0,0.0,0.0,0.0,0.0,0.00,0.00,0.00]),
_F(CARA='K_TR_D_N',
GROUP_NO='Nmaster',
VALE=[0.0,0.0,0.0,0.0,0.0,0.0]),),);
N_mass=AFFE_CARA_ELEM(MODELE=CylModel,
INFO=1,
DISCRET=(_F(CARA='M_TR_D_N',
GROUP_NO='Nmaster',
VALE=[1,0.0,0.0,0.0,0.0,0.0,0.0,0.00,0.00,0.00]),),)
Restrict the master node to act as a hinge by restricting all DOFs to zero except the rotation axis, in this case rotation around the x axis that is free:
fixNmast=AFFE_CHAR_MECA(MODELE=CylModel,
DDL_IMPO=(_F(GROUP_NO='Nmaster',DY=0.0,DX=0.0,DZ=0.0,DRY=0.0,DRZ=0.0),),)
Apply the RBE3 constraint between the cylinder area (defined by NPcyl) and the master node. This creates a connection between the master node and the surface without adding additional stiffness to the surface:
nodeRBE3=AFFE_CHAR_MECA(MODELE=CylModel,
LIAISON_RBE3=_F(GROUP_NO_MAIT='Nmaster',
DDL_MAIT=('DX','DY','DZ','DRX','DRY','DRZ',),
#DDL_MAIT=('DRZ',),
GROUP_NO_ESCL='NPcyl',
DDL_ESCL='DX-DY-DZ',
COEF_ESCL=1,),);
Apply the boundary conditions and loads to the model by the EXCITE keyword and add the previously defined fixNmast (boundary condition) and nodeRBE3 (RBE3 constraint). Since the node is a discrete element we have to add the CARA_ELEM to the MECA_STATIQUE command:
result=MECA_STATIQUE(MODELE=CylModel,
CHAM_MATER=Amat,
CARA_ELEM=N_stmass,
EXCIT=(_F(CHARGE=fixNmast,),
_F(CHARGE=bcforce,),
_F(CHARGE=presTop,),
_F(CHARGE=nodeRBE3),),);
The two remaining excitations bcforce (displacement, that seems a logical name for this) and presTop (pressure on top surface, that, once again, seems a logical name) are standard loads applied to the model.
The results - displacements
The results are been processed by Paravis (in contrast to the results above that are obtained from postpro).
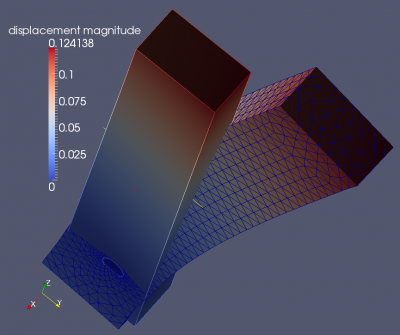
Below. This figure shows the rotation around the hole. The top right edge moves 0.1 [mm] to the right (by a boundary condition on that edge). The RBE3 constraint makes the rotation smooth and as expected.
Below. Here the previous load case (white elements) and an additional pressure on the top surface (500 bar, blue elements) are shown. We see a small distortion of the hole that shows that the RBE3 constraint does not add any additional stiffness to the surface. Due to the asymmetric of the hole the beam is slightly bend by the surface pressure. Including the original configuration is shown below:
Below. The figure on the right gives a detailed view of the area around the hole (white: no deformation, brownish: only 0.1 [mm] displacement on the top, blue: displacement and surface pressure.
Arbitrary angle of rotation
[this need adaption I guess ... although the principle is correct]
Using the LIAISON_DDL keyword we can define an arbitrary vector to rotate around. For rotating around the vector [1,1,0] we can use the following command:
fixNmast=AFFE_CHAR_MECA(MODELE=CylModel,
DDL_IMPO=_F(GROUP_NO='Nmaster',DY=0.0,DX=0.0,DZ=0.0),
LIAISON_DDL=(_F(GROUP_NO=('Nmaster','Nmaster','Nmaster',),
DDL=('DRX','DRY','DRZ'),
COEF_MULT=(1.0,-1.0,0.0),
COEF_IMPO=0.0),
_F(GROUP_NO=('Nmaster','Nmaster','Nmaster',),
DDL=('DRX','DRY','DRZ'),
COEF_MULT=(0.0,0.0,1.0),
COEF_IMPO=0.0),),)
that defines the rotation around the master node Nmaster. The two -arbitrary- vectors at COEF_MULT are perpendicular to the rotation axis [1,1,0]. Hence the two dot products prevents rotations in the directions perpendicular to the axis of rotation:
- <[Rx Ry Rz]><[1.0, -1.0, 0.0]> = +1*Rx -1*Ry = 0 --> Rx = Ry and
- <[Rx Ry Rz]><[0.0, 0.0, 1.0]> = +1*Rz = 0 --> Rz = 0
and that is what the LIAISON_DDL establishes.
View below: displacements of the bar with rotation axis [1,1,0] and displacement of 0.1 [mm] at the top right edge. This introduces some torque within the bar.
Views below: figure is yz view and right figure is xz.
Input files for the FE Analysis
Download the files here:
- >>>Media:kw_blockrot_pythonlist.zip for C-Aster version 10-
- >>>Media:kw_rotation_cylinder_ca11.zip for C-Aster version 11
Input files:
- Python script for defining the geometry and mesh (geom_mesh_blockrot.py), load by File --> load script (cntrl T in the object browser), refresh (F5) after running
- Save the mesh file by right clicking in the object browser by right clicking on the mesh name Mbcyl; select Export to MED and accept or change the default values (v11 saves mesh file automaticly in working directory)
- command file (block_cyl.comm)
- within the command file the Python script CA_geometry.py is called:
- ddl_condition = RotationAxisBC(Cmesh,'Ncyl',P1,P2,info) to apply the cylindrical boundary condition.
A short discription:- Cmesh: CA mesh, eg from Cmesh=LIRE_MAILLAGE(UNITE=20,FORMAT='MED',);
- 'NCyl': nodes that are restricted to the rotation boundary condition
- P1, P2: numpy arrays that define the axis of rotation
- info: [0|1|2] control for printing additional information
- The file also contains a procedure to apply a variable pressure on eg shell elements and defining a variable thickness to shell:
- ddl_condition = RotationAxisBC(Cmesh,'Ncyl',P1,P2,info) to apply the cylindrical boundary condition.
- ASTK file (cylrot.astk, you need to edit the path to your requirements ...)
- export file cylrot.export
[Remark:
Since Salome between version doesnot keep the same counting of geometry objects (which is quite annoying) one of the line definitions in the latest version is 'corrupt' (ie not correct) so I need to update the geometry and meshing files of the block. Adjusted]
References
CodeAster documentation:
[Document u4.44.01- AFFE_CHAR_MECA, page 20/109]
[Document u1.03.02 - Methodes Python d'access aux objects Aster - french]
CodeAster forum:
[Using python with Aster]
[Applying nodal forces node by node]
[Accessing Mesh Data Structure]
Input files for the FE Analysis and references
Earlier version Code Aster 9&10
Node selection performed in Salome
Input files:
- Python script for defining the geometry and mesh (blockrot4.py), load by File --> load script (cntrl T in the object browser), refresh (F5) after running
- Save the mesh file by right clicking in the object browser by right clicking on the mesh name Mbcyl; select Export to MED and accept or change the default values
- ASTK file (cylrot.astk, you need to edit the path to your requirements ...)
- command file (blockb.comm)
Download the files here:
- blockrot4.py and blockrot6.py basicly perform the same operation: selecting nodes on the cylinder. Though the way it is implemented is quite different: blockrot4 depends on the measures of the geometry whereas blockrot6 directly selects the nodes on the cylinder area by filters. See also [Salome] for more reference (and thank you JMB for the question asked there).
- blockrot6.py basicly construct the geometry and selects nodes on the cylinder. blockrot6.py directly selects the nodes on the cylinder area by filters. See also [Salome] for more reference (and thank you JMB for the question asked there).
- blockrot7.py writes the liaison_ddl information to a file. Remember to change the path at line 109 to a suitable value for your system.
File with the RBE3 constraint and rotation defined by master node:
- >>>Media:kw_rotcylrbe3.zip (update file needed)
Reference:
[AFFE_CHAR_MECA, page 20/109]