Contrib:KeesWouters/Homard/beam
Contents
Mesh refinement of a beam based on displacement
This contribution mainly focuses on the use of Salome, Code Aster and its macro command MACR_ADAP_MAIL. So I do not focus on the results and the mechanical justifications of the code that has been used. So no guarantee that the results will be correct up to five decimal places, which they are probably not. I do hope though that this information is useful. For me it has been, because I had to think about some commands and look through the documentation and learn from that. In case of mistakes, errors or remarks, please notify me, or better, you are invited to correct or edit them yourself. Enjoy.
The geometry
The geometry and the mesh of the construction
As usual the geometry is very simple in order not to disturb the issue we would like to show with other difficulties. Here we focus on how the refinement of a beam will be performed. In this case an axial loading on a beam takes place and the refinement is based on the axial displacement. Then it is very easy to follow the refinement process.
The geometry is defined in a python script (for download see end of this contribution) and can be loaded into Salome Geometry module by File --> Load script (or ctrl T in the object browser window). Right click Refresh or push F5 after loading if necessary.
- overall dimension: [x,y,z] = [1.0, 23.0, 2.0] mm
The mesh consists of coarse, tetrehedral elements to start with.
The bottom axial plane Afix is fixed in all direction, on the top axial plane Apres an axial displacement of 0.2 mm is prescribed.
The refinement command
Normally the refinement of the mesh will be based on and (stress) error estimation. Here we base the refinement on the axial displacement DY of the beam. The command for this is:
# adapt the initial mesh mbeam Mesh0
MACR_ADAP_MAIL(MAILLAGE_N=Mesh0, # initial mesh
MAILLAGE_NP1=CO('Mesh1'), # Mesh1 is not yet defined, so us CO'..' operator
ADAPTATION='RAFFINEMENT', # method of refinement
RESULTAT_N=result0, # refine based on this result
#INDICATEUR='ERRE_ELEM_SIGM', # and this result field
#NOM_CMP_INDICA='NUEST', # error estimation
#NOM_CMP_INDICA='ERREST', # error estimation
INDICATEUR='DEPL', # and this result field
NOM_CMP_INDICA='DY', # error estimation
CRIT_RAFF_PE=0.50, # 0.50 --> 50 % refined mesh
QUALITE='OUI',
CONNEXITE='OUI',
TAILLE='OUI',);
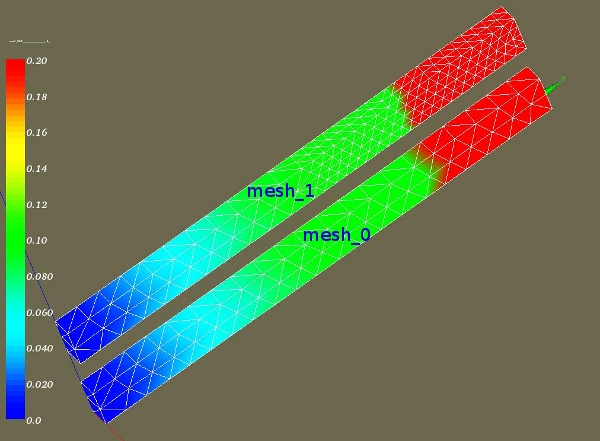
where the field INDICATEUR is now DEPL and the component field NOM_CMP_INDICA is DY. The number of elements to be refines is set to 0.50 or 50 % by the parameter CRIT_RAFF_PE=0.50. This yields the following refined Mesh1.
The mesh refinement nicely starts at the centre of the beam, in accordance with the expectation that 50 % of the largest DY displacements will start from there to the top plane.
Other examples
In the picture above, the bottom beam is the original mesh.
The second, coloured mesh is refined with CRIT_RAFF_PE=0.20 or starting at 20 % of the top.
The third mesh is the previously described refinement with 50 %: CRIT_RAFF_PE=0.50
The fourth mesh is refined at 100 % of the elements: CRIT_RAFF_PE=1.00
The top meshes 5 and 6 are successive refinements with 50%. Mesh 5 is the same as mesh number 3. This mesh is again refined at 50 % to obtain mesh 6.
This picture shows the wire frame representation of the original mesh and the refinements with 20, 50 and 100%.
Zone refinement
Various methods to define the element to be refinement are possible by the Homard macro command MACRO_ADAPT_MAIL. So far we only used the keyword 'RAFFINEMENT': ADAPTATION='RAFFINEMENT' and a result field e.g. INDICATEUR='ERRE_ELEM_SIGM' and component the NOM_CMP_INDICA='ERREST'. For ADAPTATION with a result field it is possible to choose:
- RAFFINEMENT, a field (INDICATEUR) and CRIT_RAFF_PE=0.20,
- RAF_DERAF a field (INDICATEUR) and CRIT_RAFF_PE=0.30, CRIT_DERA_PE=0.20
- DERAFFINEMENT a field (INDICATEUR) and CRIT_DERA_PE=0.20
DERAFFINEMENT makes the mesh courser, but never more than the initial mesh (niveau 0).
Other parameters that can be used with ADAPTATION are:
- 'RAFFINEMENT_ZONE'
- 'RAFFINEMENT_UNIFORME '
- 'DERAFFINEMENT_UNIFORME '
- 'RIEN'
These keywords perform on a geometrical area without a result field.
The easiest to use is probably 'RIEN', which, effectively, leaves the mesh unchanged and might be used to impress your boss who is being impatient.
'DERAFFINEMENT_UNIFORME' refines the whole mesh.
Using 'RAFFINEMENT_ZONE' needs a zone defined by the six corner coordinates (meaning [x1,y1,z1] of one corner and [x2,y2,z2] of another corner, thereby defining a hexahedral zone) or the centre and radius of a ball (defining a spherical zone). Based on the beam calculation, you can add c.q. change and add the following commands at the top of the command file:
Meshm2=LIRE_MAILLAGE(UNITE=20, # Mesh minus 2
FORMAT='MED',
NOM_MED='mbeam',
INFO_MED=2,
INFO=1,);
MACR_ADAP_MAIL(INFO=2,
ADAPTATION='RAFFINEMENT_ZONE',
MAILLAGE_N = Meshm2, # Mesh minus 2
MAILLAGE_NP1 = CO("Meshm1"), # Mesh minus 1
ZONE=(_F(X_MINI = -0.30,
X_MAXI = 1.30,
Y_MINI = 2.00,
Y_MAXI = 6.00,
Z_MINI = -0.30,
Z_MAXI = 2.30,),),
QUALITE='OUI',
CONNEXITE='OUI',
TAILLE='OUI');
MACR_ADAP_MAIL(INFO=2,
ADAPTATION='RAFFINEMENT_ZONE',
MAILLAGE_N = Meshm1, # Mesh minus 1
MAILLAGE_NP1 = CO("Mesh0"), # Mesh 0
ZONE=(_F(X_CENTRE = 0.50,
Y_CENTRE =17.50,
Z_CENTRE = 1.00,
RAYON = 2.50,),),
QUALITE='OUI',
CONNEXITE='OUI',
TAILLE='OUI');
The first command now reads the initial mesh 'Meshm2'.
This 'Meshm2' is refined within the geometrical box [xmim xmax ymin ymax zmin zmax] = [-0.3 1.3 2.0 6.0 -0.3 2.3] (second command).
The generated 'Meshm1' is refined within a ball with centre and radius [xc yc zc; radius] = [0.5 17.5 1.0; 2.5]. The result mesh is 'Mesh0' (third command).
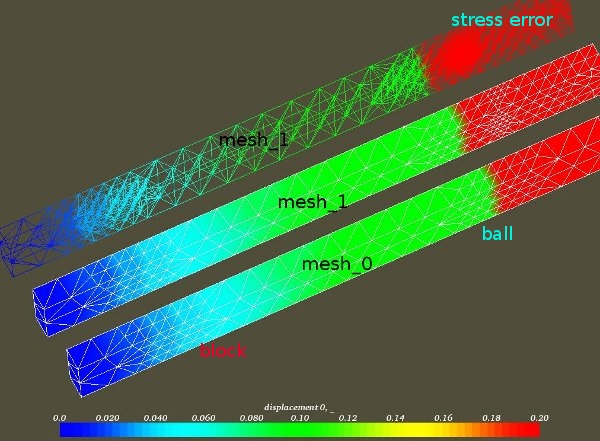
Picture of the zone refinement
The bottom beam shows the mesh that has been refined by the two zone commands, block and ball.
The centre and top beams represent 'Mesh1' after refinement with the results based on the y displacement.
The centre is the surface frame representation, the top beam is the insideframe representation.
Download files
This zip contains the following files
- python geometry and mesh file geom_mesh_block.py. Load this file in Salome by File --> Load script (cntrl T)) and right select refresh (F5) in the object browser. Export the med file in the mesh module under mbeam.med for further processing by Code-Aster, controlled by ASTK.
- command file for Code-Aster: refine012.comm
- astk file for file control by ASTK: refine012.astk
- export file, generated by ASTK: refine012.export
The result files res0.med, res1.med and res2.med can be viewed in the post processor module of Salome by File --> Import --> res<x>.med or cntrl I in the object browser. Importing it into the mesh module can be useful to check e.g. the number of elements. Note that the result files are stored in different files here (res0, res1 and res.med). It is quite as easy to store them in one file, say refres.med. Then only one file needs to be defined in ASTK. All the results are stored in seperate fields in this file under mesh_0, mesh_1 and mesh_2. This depends on the names given in the command file. Matter of taste I guess.
The command file is with two successive refinements with 50 % of the elements. Different refinements can easily be obtained by changing the value of CRIT_RAFF_PE=0.50 in the MACR_ADAP_MAIL(..) command.
The files with zone refinement
Same a above, but with zone refinement.
- geom_mesh_block.py
- zone_refine.comm
- zone_refine.astk and
- zone_refine.export
Practically, only the two refinement command at the beginning have been added.
Have fun.
That's it for now.
At the end of the winter of 2009/2010.
Kees