Contrib:BondMatt/TurbulentPipeFlow
Contents
- 1 Introduction
- 2 Software Versions:
- 3 Fluent Tutorial
- 4 Geometry/Mesh
- 5 Boundary Conditions - Code Saturn
- 6 Results - Code Saturne
- 7 Code Saturne - Default Solver Settings
- 8 Results - Code Saturne - Default Solver Settings
- 9 Results - Code Saturne - Scalable Wall Function
- 10 Results - Code Saturne - Scalable Wall Function & Upwind finite difference schemes
- 11 Results - Code Saturne - Scalable Wall Function & Steady Flow Management Relaxation Parameter
- 12 Results - Code Saturne - Scalable Wall Function & Pressure Increase Relaxation (Global) Parameter
- 13 Revised Mesh
Introduction
This tutorial will attempt to follow as closely as possible the turbulent pipe flow Fluent tutorial available on Cornell's website. However, it will use the open source CFD solvers Code Saturne and OpenFOAM.
The model is very similar to the laminar pipe flow tutorial with the exception of the dynamic viscosity which is two orders of magnitude smaller at 2E-5kg/m/s.
Therefore, the Reynolds number, or ratio of inertial to viscous forces, is two order of magnitude higher with a value of 10 000. The flow will clearly be turbulent since viscous forces are minimal and damping will be essentially non existent. Laminar flow can be experimentally observed at much larger Reynolds numbers (up to approximately 100 000 if my memory serves me correctly) with very smooth pipes (I believe ceramics were used in some research) and controlled conditions. This makes sense, with no external disturbance and very low pipe roughness perturbations will be minimal.
Software Versions:
Ubuntu 8.04 LTS
Salome V5.1.3
Code Saturne V2.0 (GUI)
OpenFOAM 2.0
Fluent Tutorial
The Cornell University Fluent tutorial can be found here [1].
Is it just me or are the variables 'd' and 'D' reversed in their figure?
Geometry/Mesh
Geometry
The geometry is identical to the previous tutorial. I was hoping to convert the OpenFOAM/snappyHexMesh coarse hexahedron mesh for use with Code Saturne but there is no direct conversion tool in OpenFOAM or that I could find online. It might be possible to manually convert the mesh if the file is ASCII text and perhaps I will try to do this and add it. For now I will create a mesh in the MED format in Salome. I may try to convert it to a format compatible with OpenFOAM. I think I still have the old Code Saturne files for the laminar tutorial but they would be on a laptop with a dead GPU.
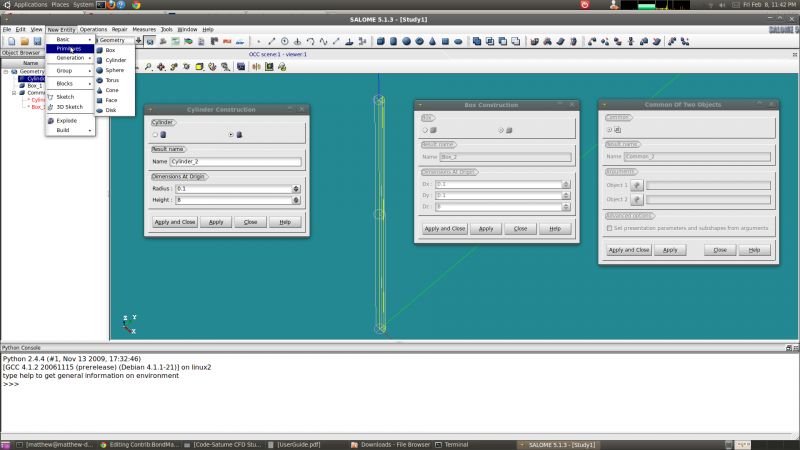
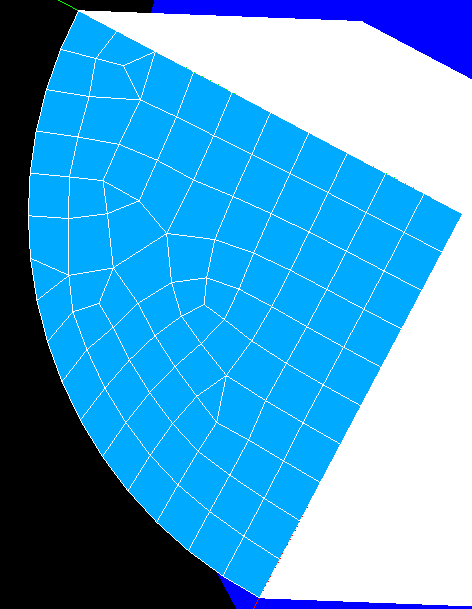
My first step was to create a quarter of a cylinder with a radius of 0.1 meters and a length of 8 meters. This was done by first creating a cylinder with the 'Create a cylinder' tool which can be accessed through a toolbar (at least in my installation) or through the 'New Entity' menu and 'Primitives'. I also created a box with dimensions of 0.1 X 0.1 X 8 meters. This was followed by a Boolean operation to extract the common or overlapping region.
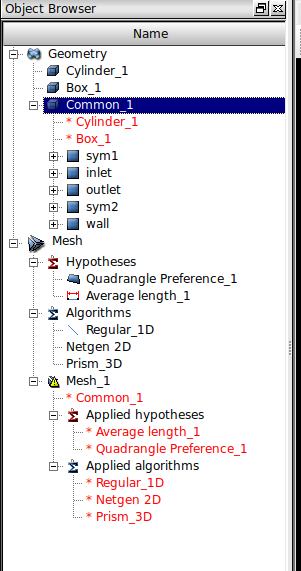
The next step was to 'Explode' the entity created by the Boolean operation through the 'New Entity' menu. The quarter cylinder was exploded into faces so that they could be re-named for boundary conditions. Mesh cells and/or nodes associated with these surfaces can be identified and grouped by Salome at the meshing stage for boundary conditions in the solver. Reasonable names like 'wall', 'sym1', 'sym2', 'inlet', and 'outlet' were used.
Mesh
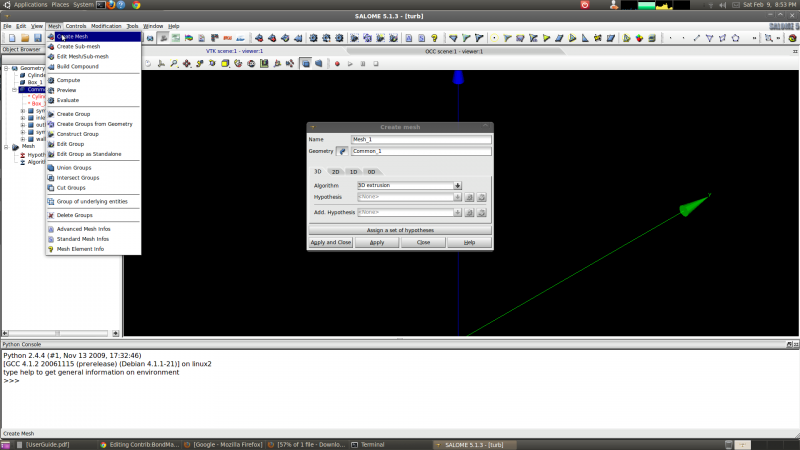
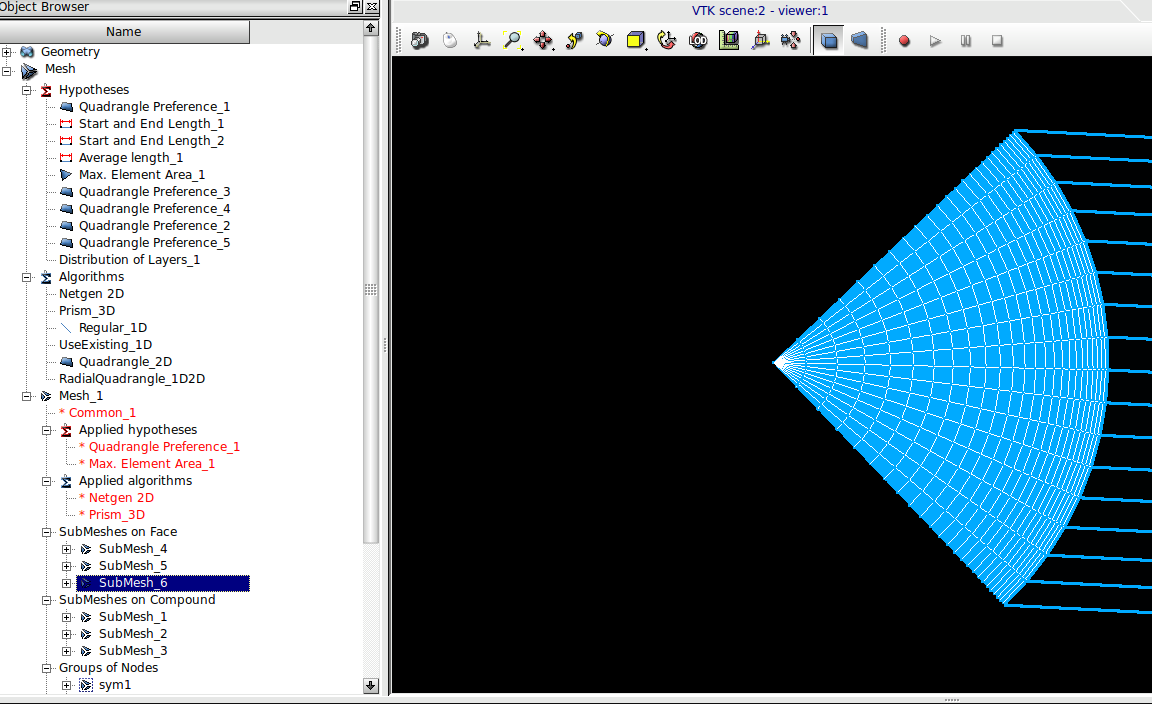
Switching to the meshing interface, the procedure for creating a mesh was to first create global meshing settings by going to the Mesh menu and selecting Create Mesh. In the dialog box that pops up the Geometry entity Common_1 is selected and the 3D meshing Algorithm '3D extrusion' is selected (shown in the figure below).
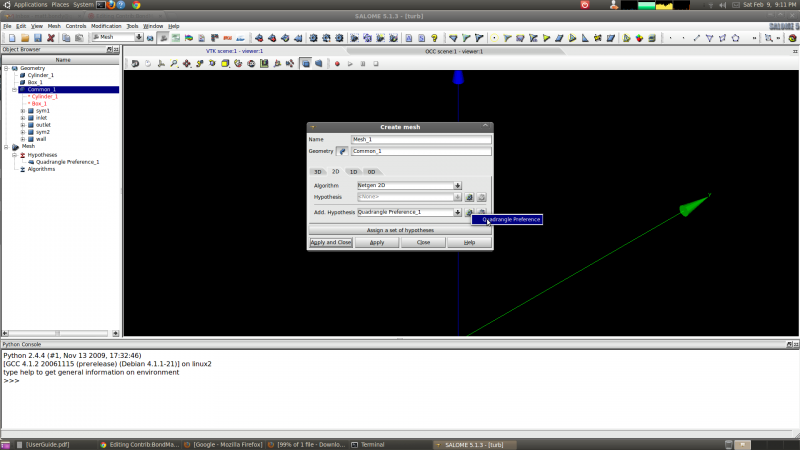
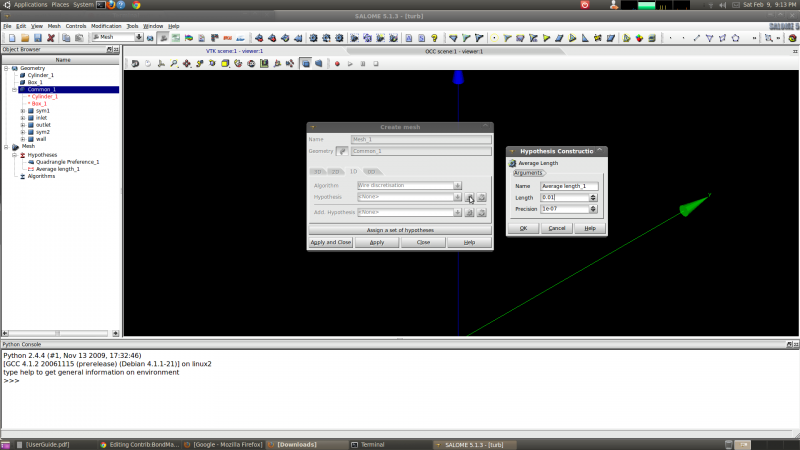
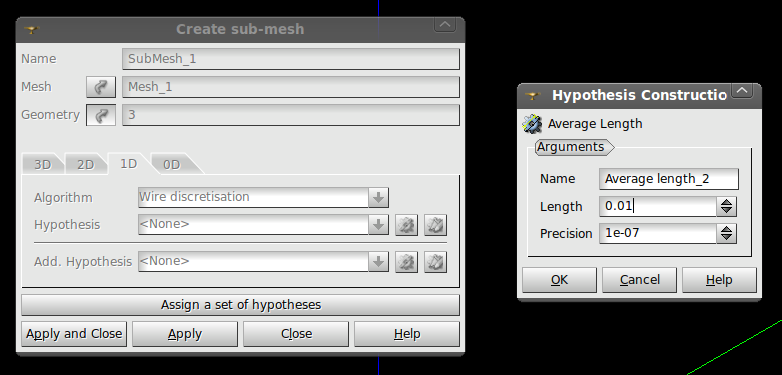
The global 2D mesh setting is (or can be) Netgen 2D with the Quadrangle Preference added hypothesis. The 1D meshing setting can be Wire Discretization with the Average Length hypothesis with the length set to 0.01.
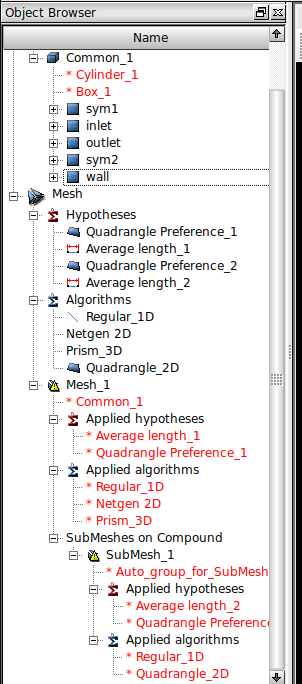
The object browser should end up looking something like:
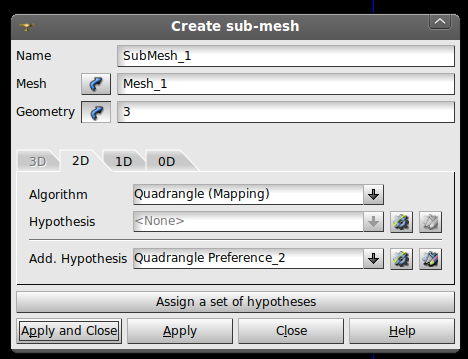
The next step I took was to create sub meshes with nice, regular quadrangle meshes. Go to the Mesh menu and select Create Sub-Mesh. Pick the mesh previously created (probably called Mesh_1) and the geometry entities that were created by exploding the solid quarter cylinder into faces. However, do not pick all of these faces. Only pick the faces that will be planes of symmetry and the wall of the pipe. I use the 2D algorithm Quadrangle Mapping with the Max Element Area hypothesis (max area of 0.01 * 0.01 meters, input 0.0001) and the Quadrangle Preference Add. Hypothesis. I used the 1D algorithm Wire Discretization with an Average Length hypothesis (set to 0.01 meters). Note I forgot the Max Element Area hypothesis at the time and so it is not in the figure.
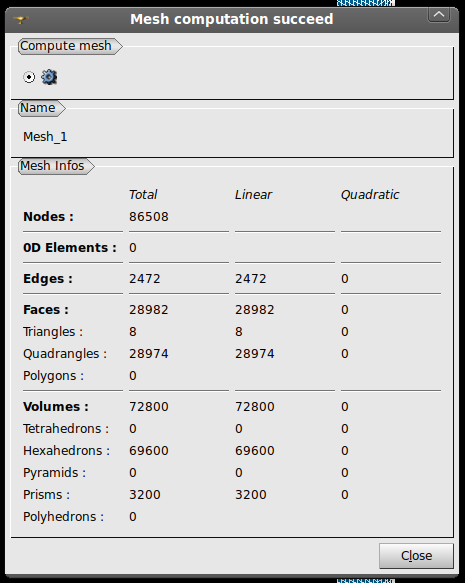
Finally, compute the mesh by, at least one way of doing it, right clicking on Mesh_1 and selecting 'Compute'. It should compute successfully and there should be no tetrahedron elements. Most elements are hexahedron or elements with 6 sides where each side has 4 edges and 4 vertexes. There will likely be some 'Prisms' or 'Wedge' elements (perhaps more properly called pentahedrons?).
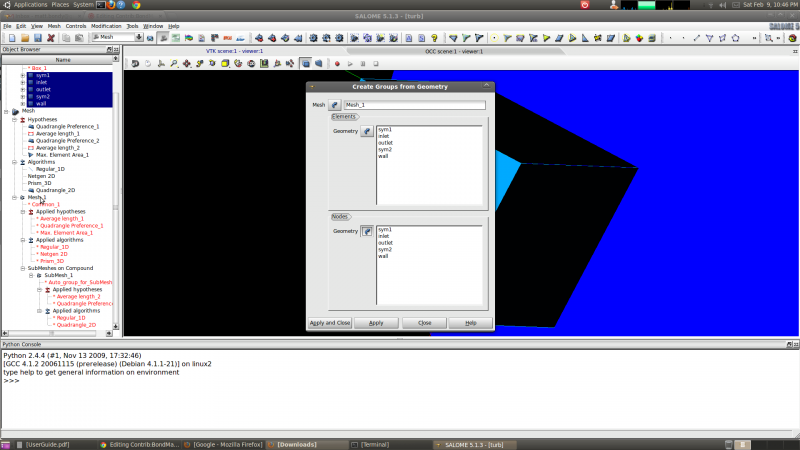
The only step left is to create element/cell face and node groups for boundary conditions. This can be done by right clicking on the entry for the mesh in the tree (probably Mesh_1) and selecting Create Groups from Geometry. Then select the geometry faces creating by exploding the quarter cylinder and named after boundary conditions (BCs).
The resulting mesh can be exported in the MED format for use with Code Saturn (right click on Mesh_1 and Export to MED File or in the File menu 'Export' then 'to MED File'.
Boundary Conditions - Code Saturn
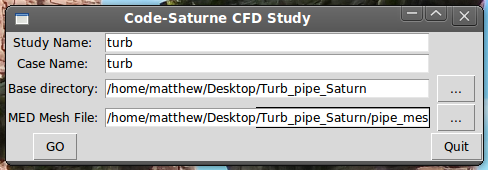
I start off using the Code Saturne wizard in CAELinux. I imagine it is fairly easy to just start creating the solver input file in the Code Saturne GUI. Looking at the Code Saturne website I am quite curious about any updates and the pre-processor they refer to separately from the GUI: http://code-saturne.org/cms/download/2.0
Version 2.0 looks to be the most recent proper release but there were newer beta releases. I do not recall being able to find that website last I looked but colour me impressed!
The case creation wizard in CAELinux looks like this:
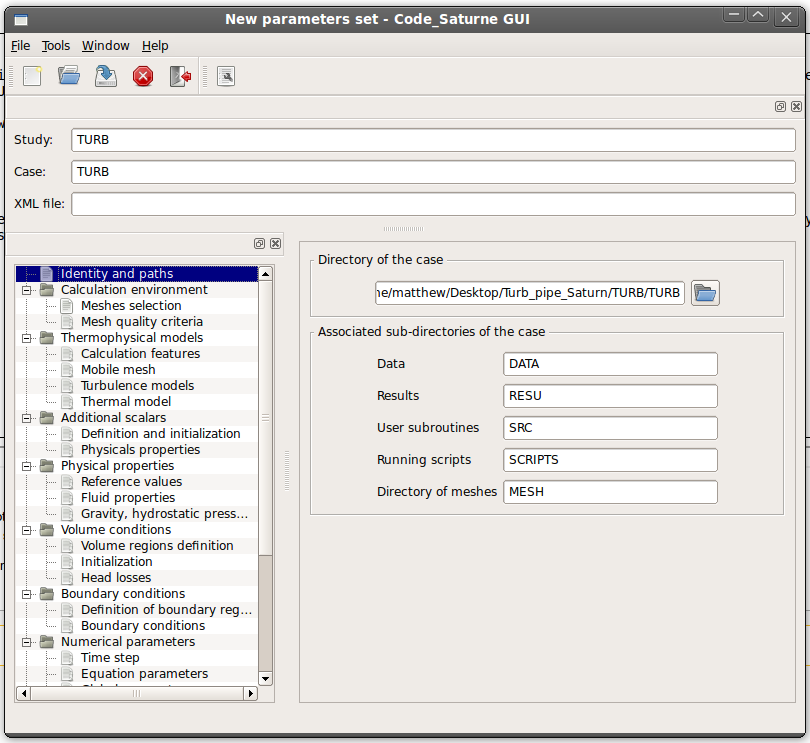
Clicking 'GO' opens what I imagine is the Code Saturne GUI (or the pre-processor?) Clicking on the 'New file' icon fills in the entries on the first page automatically (which I imagine is dependent upon using the wizard which may or may not come with the files on the website just linked to).
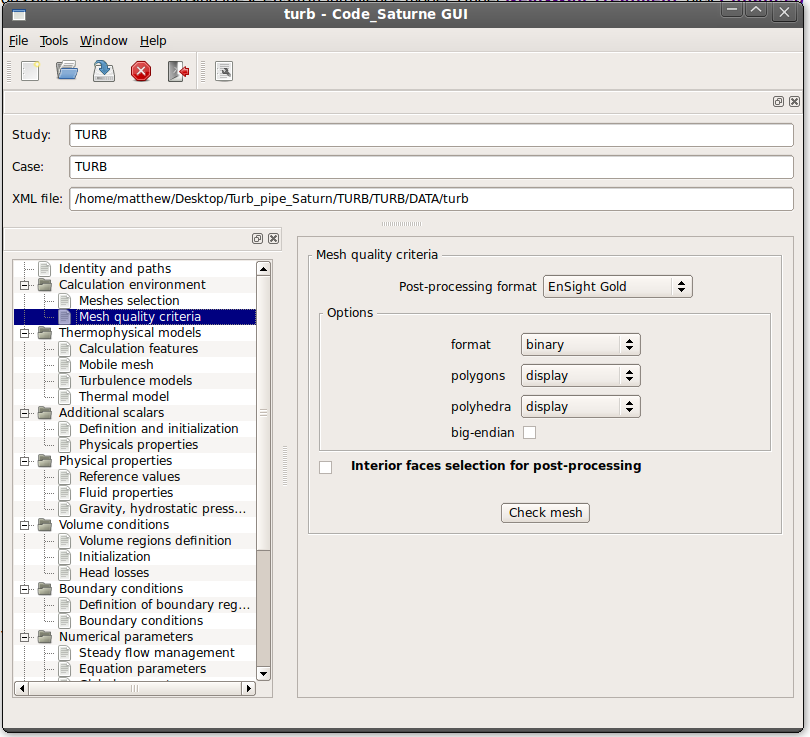
Moving through the list of settings that can be modeled from top (Identity and paths) to bottom (Prepare batch calculation) the first critical item is under 'Mesh quality criteria'. While probably a good idea in general, the mesh quality must be checked (as far as I can tell) to read in the boundary condition grouped faces/nodes created in Salome. Clicking on Check mesh performs some sort of check of the mesh and asks the user to save a file. This file will be used later.
This quality check is not so impressive having just finished the tutorial on laminar pipe flow with OpenFOAM which had much more extensive mesh checking. However, I really have no idea what I am doing so I hesitate to make these statements. I have little experience with CFD. I have actually considerably more experience with non-linear structural finite element analysis but user KeesWouters has covered related topics in CAELinux quite extensively. I doubt I could convince myself to work on this topic at my leisure anyways, with CFD I have more to learn.
The next setting that can be modified is 'Calculation features' in the 'Thermophysical models' section. I changed the flow algorithm to steady flow. This might not be necessary. An approach like that used with OpenFOAM where a termination time large enough to reach a steady state could be used. In fact it might be difficult to use a steady flow model with known turbulence. In the case of von Karmann vortex shedding I imagine a solver would have difficulty in converging to a solution without allowing dependence on time: http://www.youtube.com/watch?v=IDeGDFZSYo8
Turbulence modeling is not necessary (look up direct numerical simulation: http://en.wikipedia.org/wiki/Direct_numerical_simulation also this Ars Technica article is interesting: http://arstechnica.com/science/2011/07/what-makes-the-fuel-go-boom-turbulence/). Turbulence modeling is a way of modeling the energy dissipation of eddies without modeling the eddies. Modeling the eddies could require a very large number of very small cells in the mesh. The smallest eddies of turbulent flow have characteristic lengths on the order of the Kolmogorov microscales: http://en.wikipedia.org/wiki/Kolmogorov_microscales Turbulent flow is a series of cascading eddies (eddies producing yet smaller eddies) down to eddies of the sizes predicted by Kolmogorov. If the model uses the un-modified Navier Stokes equations it must model all of these eddies to properly predict energy dissipation. However, if eddies smaller than a given size are not of interest (and in many cases, like flow in a pipe, they are essentially just noise in terms of the minor effect on average axial velocity fluctuation) some sort of mathematical model of how this energy is dissipated can be added.
The Navier Stokes equations essentially consist of Newton's second law applied to an element of fluid (although usually re-phrased as the flow of fluid through a volume, hence the name finite volume method for the numerical procedure used to solve the equations). These equations are also usually referred to as momentum equations as they describe the conservation of momentum (Newton's second law states that the sum of the forces on a body is equal to the derivative of the momentum with respect to time, only when the mass is constant does this simplify to mass * acceleration). This gives three similar equations, one for each principal direction. There is also the continuity equation which enforces the conservation of mass. Turbulence modeling adds at least one equation (and requires the use of modified the Navier Stokes equations???). In the case of temperature change an equation for the conservation of energy is added (similarly equations are added for modeling phenomenons like chemical reactions, etc.)
I do not recall the default turbulence model in Code Saturne but it might be the k-epsilon model (or turbulence modeling might not be enabled by default). The Fluent tutorial I am following uses a 2 equation k-epsilon model which should be consistent with the model in Code Saturne. With this turbulence model k is the turbulent kinetic energy and epsilon is the dissipation or physical scale (good resource here: http://www.cfd-online.com/Wiki/K-epsilon_models). An excellent resource is the Fluent users guide: https://www.sharcnet.ca/Software/Fluent12/html/th/node58.htm The k-epsilon model is well suited for industrial flow which I interpret to mean internal flow for reasonable conduits. The model includes a set of constants which by default, at least in Fluent, are set to values determined from series of experiments. Looking at page 9 of the Code Saturne theory manual their implementation of the k-epsilon model uses the same default parameters: http://code-saturne.org/cms/sites/default/files/theory-2.0_0.pdf I am not clear on whether or not they can be changed easily.
I also change the dynamic viscosity to be consistent with the Fluent tutorial (Fluid properties in the Physical properties section) to 2E-5 Pa*s. I do not recall coming across a dynamic viscosity with the units arranged like this. I like it. My trick to remember the difference between kinematic and dynamic viscosity is to recall that the units for kinematic viscosity are simple length and time units consistent with kinematic analyses of simple mechanisms to solve for displacements, velocities, etc.
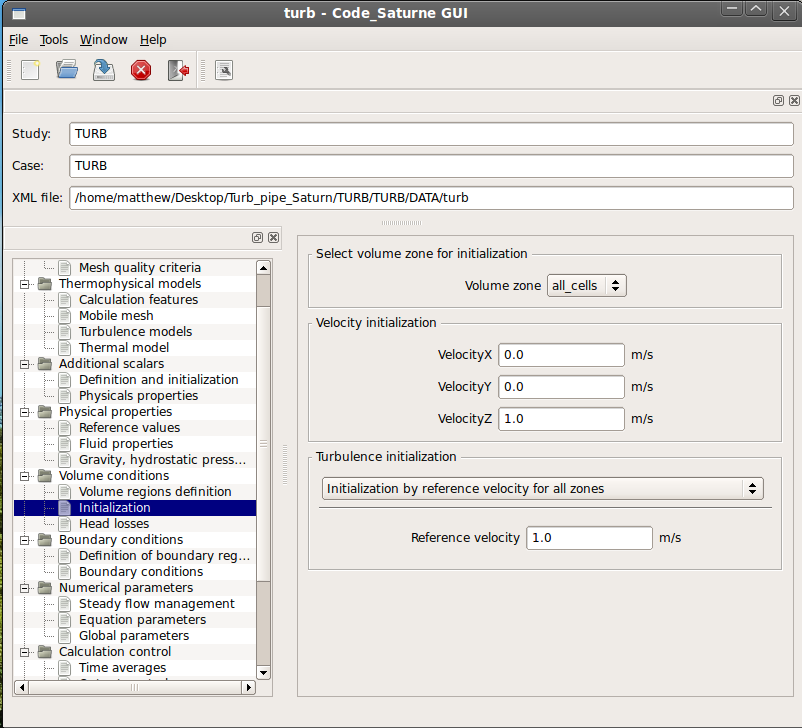
The next item changed was the velocity initialization in the z-direction (axial) to 1.0 m/s (Initialization under Volume conditions). The BC at the inlet will be 1.0 m/s at all faces of the Inlet mesh group. (I believe velocities are all determined from considering flow into and out of all cells through their faces with an average velocity at each face center, at least for any finite volume method based technique which is quite common). With the lower viscosity the boundary layer will be much smaller at the wall of the pipe and so a spatial average of axial velocity at any cross section of the pipe will be very consistent at approximately 1 m/s.
The initialization of turbulence in the Fluent tutorial was completed by specifying a turbulence intensity of 1% and a hydraulic diameter at the inlet and then initializing all cells from this value. I do not believe this procedure can be followed exactly in version 2.0 of Code Saturne but the end result (the results of the simulation) should not be different between the two CFD solvers. The turbulence boundary condition can be specified in the same way but the values cannot be used to initialize all other 'nodal' (cell center?) values. Hopefully the model converges to the same results (which of course will be the goal, one big discrepancy at the moment is the mesh, the Fluent model uses a mesh with biasing, the cells are much smaller radially near the wall than near the centerline).
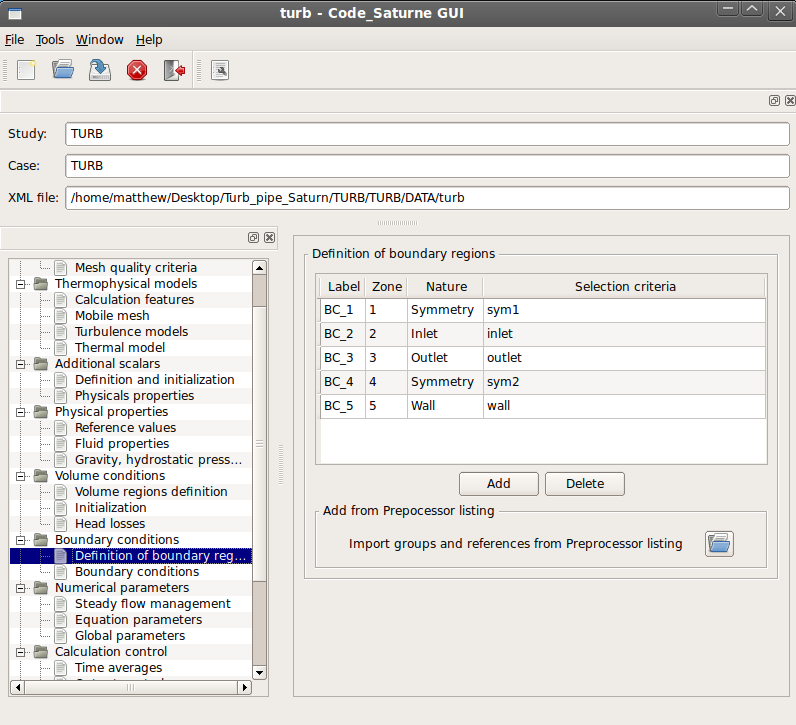
The next step was to set the boundary conditions. First, to see the cell groups created in Salome under 'Definition of boundary regions' the file that was created when checking the mesh has to be selected by clicking on the blue folder under 'Add from Preprocessor listing' (in the 'Definition of boundary regions' page of the GUI). After picking this file the page should appear as follows (the 'Selection criteria' might differ depending on how the cell groups are named).
The last item to be changed may be the Post processing format (to EnSight Gold) under Output control (in the Calculation control group). Any other format might also work fine but the Ensight Gold format works fine with Paraview which I have been using as a post processor. I tried using the default format and had some trouble getting the results to open in Paraview.
I think the following file should be sufficient to create this model with the Code Saturne GUI:
File:Turbulence tutorial xml.zip
Results - Code Saturne
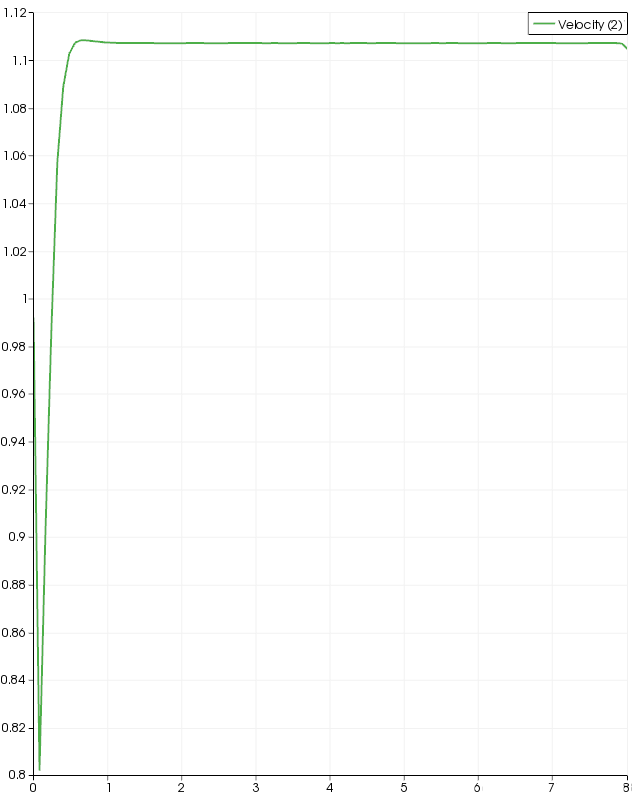
The following is the centerline velocity obtained with Code Saturne. The steady state value (1.15 m/s) is different than that obtained with Fluent (1.2 m/s). There is also an initial fluctuation of this quantity with Code Saturne that is not observed with Fluent. An interesting observation is that when post-processing in ParaView there are several time steps. I would not have expected this since I selected that the flow has reached a steady state condition. However, it is difficult to say much with any certainty without knowing more about the numerical algorithms employed and this can get quite messy in a hurry. Looking at the settings under 'Steady flow management) (in the 'Numerical parameters' category) the number of iterations is set by default to 10. Going back to ParaView there are 10 time steps. This may just be a coincidence or it could be an indication of the algorithm employed. I am less familiar with numerical algorithms in CFD but I do know that the Navier-Stokes equations are incredibly complex partial differential equations. Solving them in all but the simplest of scenarios is incredibly difficult. There is even a $1 million prize to definitively show that there exist solutions to the Navier Stokes equations under practical conditions: http://en.wikipedia.org/wiki/Navier%E2%80%93Stokes_existence_and_smoothness
In Fluent the solution is iterative at each time step but if the user specifies a steady state condition exists the software will give no indications that it is solving over time. Iterations are performed and the user can stop at any time and view the solution. Generally one views residuals for changes in average pressure, velocity, etc. and when these quantities stop changing (and produce no residuals or changes in value from one iteration to the next) a solution has been found. I imagine this is not just an indirect solver for a linear system. A linear system (Ax=B) can be solved directly (invert A and multiply by B) or indirectly (estimate x, multiply by A, assess error, repeat if necessary). A non-linear system can also be linearized or it might be of a form such that A is dependent on x and an estimate of x produces an estimate of A, solving for x as if it is a linear system gives a new estimate of A and so on. I will have to dig out a good Fluent specific textbook I have to get a refresh. I imagine Code Saturne's solver is different from Fluent's and, possibly, uses a simplified transient solver to solve steady state problems. OpenFOAM seems similar although it has a bunch of different solvers which I realyl should have put in some sort of table. A quick look through the Code Saturne user and theory manuals did not clear this up (I might need Code Saturne for Dummies, edit: I found something useful through the CS forum: File:CS pdf.pdf).
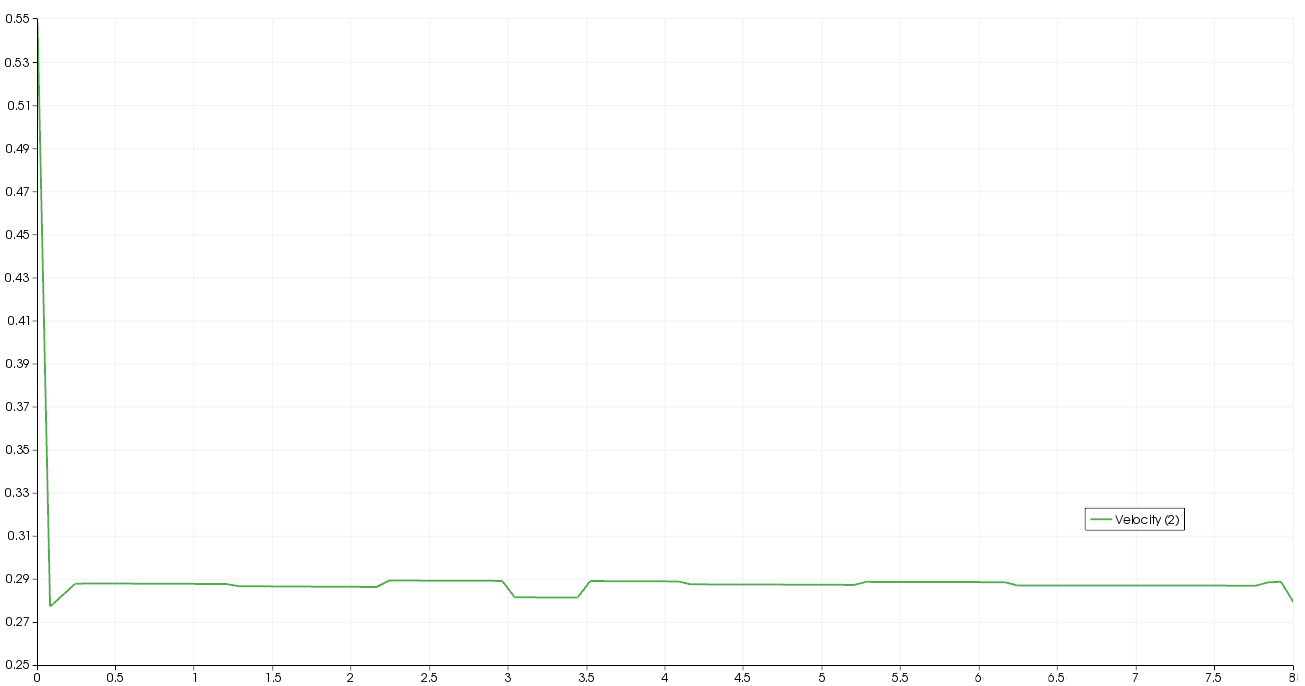
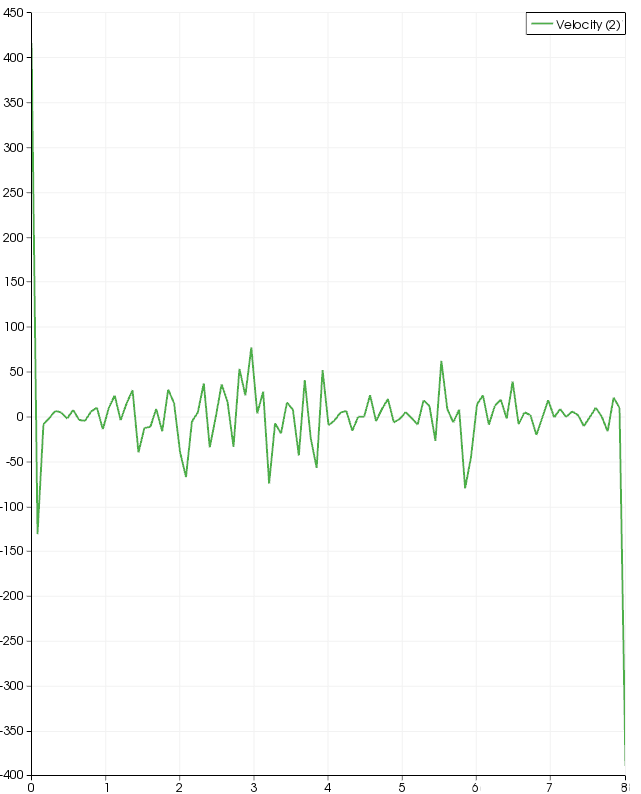
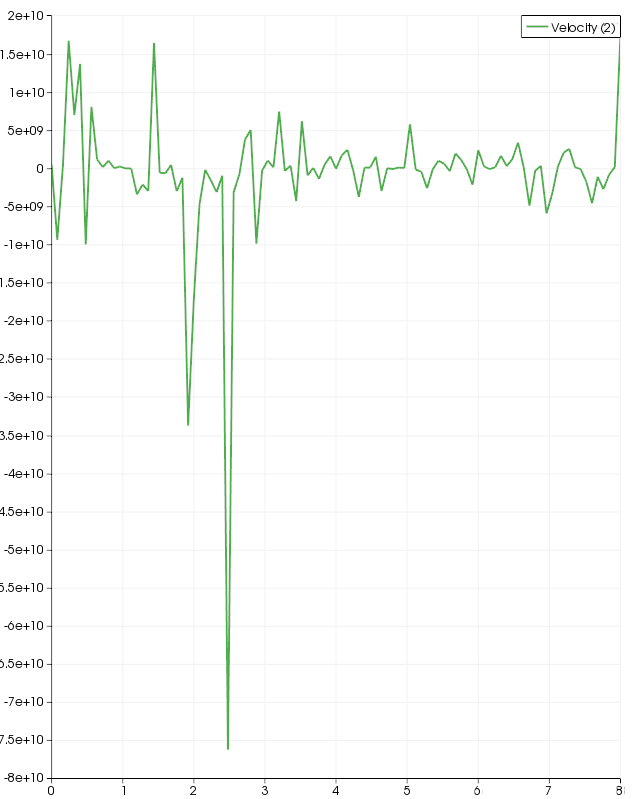
A logical next step was to create a mesh like that used with Fluent. This proved somewhat more difficult than I expected and I do not love what I ended up with. At the moment the results are also terrible but I do wonder if this is associated with an attempt to use a parallel solver. Edit: I will leave the poor results despite identifying why they occurred. The parallel processing was not to blame. After adjusting the relaxation coefficient under 'Steady flow management' more reasonable results were obtained as shown below. However, the seemingly random fluctuations in the centerline velocity stand out and beg for further investigation.
Code Saturne - Default Solver Settings
As was briefly discussed in the previous section, a good solution was not found with the default solver settings. Altering these settings yielded a better result but it was still far from ideal. After a few additional trials it was clear that a proper study of solver settings would be a suitable method for proceeding.
Default solver settings:
Relaxation coefficient: 0.9
Number of iterations (restart included): 10
Maximum number of iterations for each equation: 10000 (identical for all)
Solver precision 1e-8
Relaxation of pressure increase: 1.0
Results - Code Saturne - Default Solver Settings
With the default solver settings the following message was observed in the 'listing.XXXXXXX' file (where XXXXXXX is a number assigned to this particular set of results) in the results directory (RESU).
y-plus is the dimensionless wall distance and details on it can be found here: http://www.cfd-online.com/Wiki/Dimensionless_wall_distance_(y_plus) The CFD-online Law of the wall article is poor when compared to the wikipedia article: http://en.wikipedia.org/wiki/Law_of_the_wall An excellent Engineering Tips post on this topic: http://www.eng-tips.com/viewthread.cfm?qid=248146
The key point from that last link relevant to the CS warning message is this: "Now CFD codes assume that this viscous sublayer where u+=y+ happens between the wall and the first grid point. The first grid point is where code switches from the log-law to the viscous sublayer. Generally this switch should occur at a value of y+ somewhere around 30. If your mesh is too fine near the wall, you will get a low value of y+. This will result in overprediction of the near wall velocity. On the other extreme, if y+ is too high, it will cause the code to apply the law of the wall to the outer wake where it is not valid."
This is interesting considering the contour plot of velocity below. Near the wall the velocity is maximum and is much higher than it should be (since the Reynolds number is so high I expect an extremely large velocity gradient near the wall (zero velocity at the wall to a maximum slightly larger than 1 m/s). Using the cfd-online calculator the boundary layer thickness for this model should be approximately 10 mm which looks to be approximately the thickness of the region of erroneous maximum axial velocity (red colouring in contour plot).
So the mesh should be designed with this in mind when modeling turbulent flow. There exists this online calculator for determining the thickness of the mesh of the boundary layer at the wall: http://www.cfd-online.com/Tools/yplus.php
Edit: Additional excellent information in the Fluent user guide can be viewed here: https://www.sharcnet.ca/Software/Fluent12/html/ug/node410.htm
Going back to the Cornell Fluent tutorial the enhanced wall treatment option in Fluent is used.
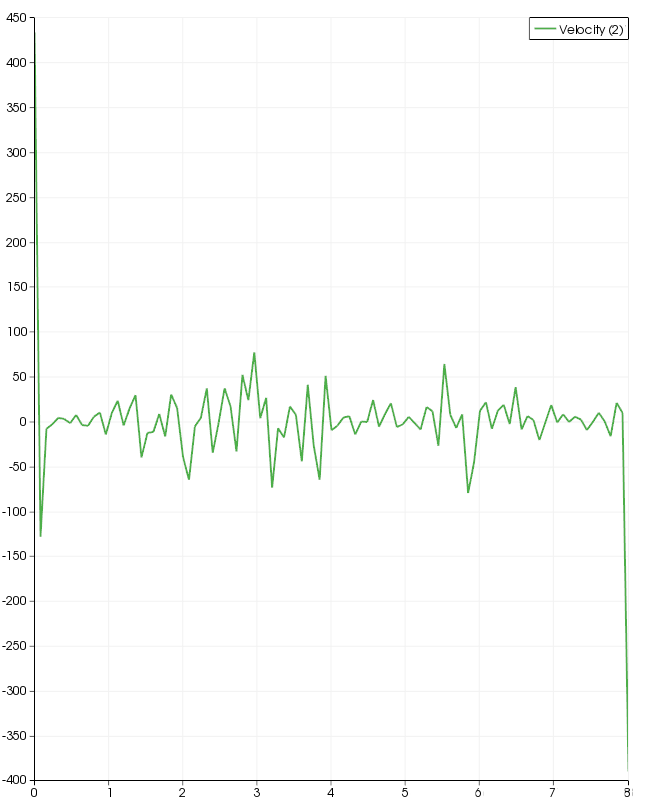
Results - Code Saturne - Scalable Wall Function
After the results of the previous section a look at the GUI for something similar to the enhanced wall functions of FLUENT led me to the Code Saturne practical users guide. On page 129 (CS v2.07) the scalable wall function option (an advanced option for the turbulence model in the GUI) is indicated to be a potential solution for modeling high Reynolds number flows on very refined meshes. I was considering a coarser mesh but I see no middle ground between my fine and coarse meshes (the cfd-online calculator predicted the boundary layer mesh needed to be approx. 10 mm thick). This also seems odd since I was under the impression the boundary layer should be resolved with a fine mesh.
This did not work particularly well. However, I have now added a picture of the refined mesh I have been trying to use. I suspect it is the mesh causing the problem although I have no specific reasoning. The message in the listing file side-tracked me but it led to some interesting and fundamental concepts of CFD.
Results - Code Saturne - Scalable Wall Function & Upwind finite difference schemes
The NS equations are partial differential equations and consist of a number of terms where quantities are differentiated over space or time. Numerical approximations of derivatives in a discretized volume consist of simple calculations like calculating the slope of a straight line.
There are three finite difference schemes commonly used: upwind, central, and backwards differencing. Hybrid differencing also exists but is less common.
Central differencing is the most accurate, numerically, of the three common schemes (considering truncation error with a Taylor series). Upwind differencing has advantages when the grid is aligned with the flow as it can identify the strong upwind influence on flow. For the current problem it seemed reasonable to try to use this scheme. However, the results are not impressive:
Results - Code Saturne - Scalable Wall Function & Steady Flow Management Relaxation Parameter
Another attempt at obtaining a reasonable solution was to adjust the relaxation coefficient under Numerical parameters / steady flow management. This parameter was set to 0.01, by default it is 0.1.
Relaxation coefficients are well suited for an example:
Let us say we have the following set of equations:
3x - 0.1y - 0.2z = 7.85
0.1x + 7y - 0.3z = -19.3
0.3x - 0.2y + 10z = 71.4
A = [3 -0.1 -0.2; 0.1 7 -0.3; 0.3 -0.2 10]; b = [7.85; -19.3; 71.4];
They can be re-arranged:
x = ( 7.85 + 0.1y + 0.2z ) / 3
y = ( -19.3 - 0.1x + 0.3z ) / 7
z = ( 71.4 - 0.3x + 0.2y ) / 10
Guess/estimate y=0 & z=0:
x = 7.85 / 3 = 2.61667
y = ( -19.3 - 0.1 * 2.61667 + 0.3 * 0 ) / 7 = -2.794524
z = ( 71.4 - 0.3 * 2.616667 + 0.2 * -2.794524 ) / 10 = 7.005610
Is this correct?
No,
3 * 2.61667 - 0.1 * -2.794524 - 0.2 * 7.005610 = 6.7283404
(should equal 7.85)
Note that in calculating z the updated estimate of y was used rather than the original estimate of y=0. Using the most recently updated values for unknowns is known as the Gauss-Seidel method. Using y=0 (not using each updated estimate for an unknown as it becomes available but waiting until an entire set of updated values is available) is called Jacobi iteration.
An iterative algorithm like this is the method used by an indirect solver. A direct solver would usually compute x = inverse(A) * b or use some other non-iterative technique. However, computing the inverse of A is computationally intensive.
Putting this in an Octave/MATLAB terminal:
y=0; z=0;
for i=1:3 x=(7.85+0.1*y+0.2*z)/3, y=(-19.3-0.1*x+0.3*z)/7, z=(71.4-0.3*x+0.2*y)/10 end
The last output of x, y, and z are the exact solution (3 iterations is the minimum to converge to this solution with the unmodified Gauss-Seidel method):
x = 3 y = -2.5000 z = 7
In this case the algorithm converges rapidly but the equations have properties well suited to the method. Note the relatively large coefficients for the diagonal of the matrix A. If for all rows the sum of the absolute values of the off diagonal coefficients is less than the absolute value of the coefficient of the diagonal the method is guaranteed to converge (such systems are diagonally dominant). Systems that do not meet this criterion may also converge.
Considering a different system: 3x - y - 2z = 7.85 x + 7y - 3z = -19.3 3x -2y + 10z = 71.4
The standard Gauss Seidel approach in Octave:
x=0; y=0; z=0;
for i=1:5 x=(7.85+1*y+2*z)/3, y=(-19.3-1*x+3*z)/7, z=(71.4-3*x+2*y)/10 end
x = 2.6167
y = -3.1310
z = 5.7288
...
x = 5.6229
y = -1.3373
z = 5.1857
The exact solution:
x = inv([3 -1 -2; 1 7 -3; 3 -2 10])*[7.85; -19.3; 71.4]
x = [ 5.6265 -1.3391 5.1842 ]
After 5 iterations with the Gauss-Seidel method the exact solution has not been achieved but it does appear to be converging to a solution. In this case over-relaxation may be worth considering to more rapidly reach the solution:
x=0; y=0; z=0;
r=1.01;
for i=1:5 x=r*(7.85+1*y+2*z)/3+(1-r)*x, y=r*(-19.3-1*x+3*z)/7+(1-r)*y, z=r*(71.4-3*x+2*y)/10+(1-r)*z end
x = 5.6246
y = -1.3361
z = 5.1854
The format for any type of relaxation is:
x_new_2 = r * x_new_1 + (1 - r) * x_old
Code Saturne does not appear to allow for over-relaxation (the steady flow management relaxation parameter has a maximum of 1.0). In my (limited) experience with Fluent and Star CCM under-relaxation is incredibly useful in obtaining a good solution.
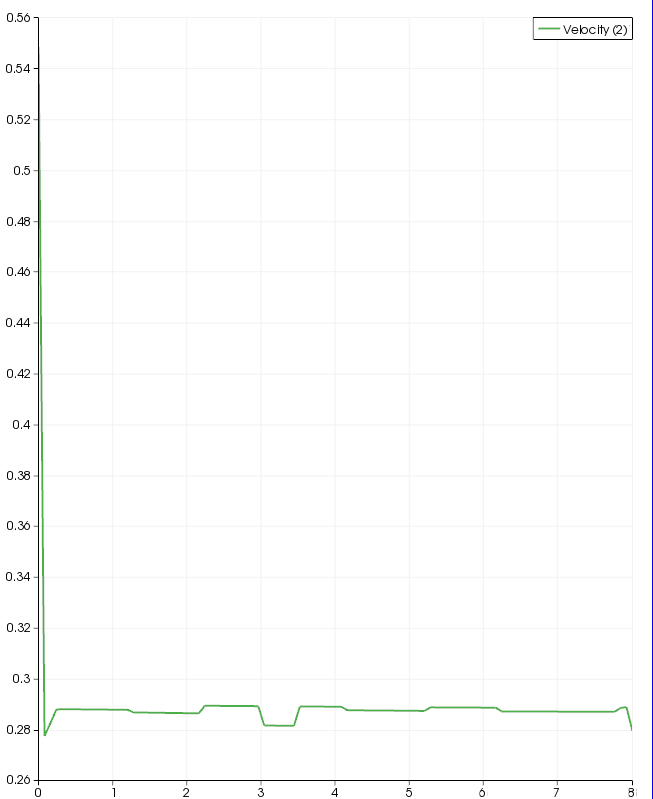
In this case, with Code Saturne, reducing the steady flow management relaxation coefficient to 0.01 yielded the following result for axial velocity:
Results - Code Saturne - Scalable Wall Function & Pressure Increase Relaxation (Global) Parameter
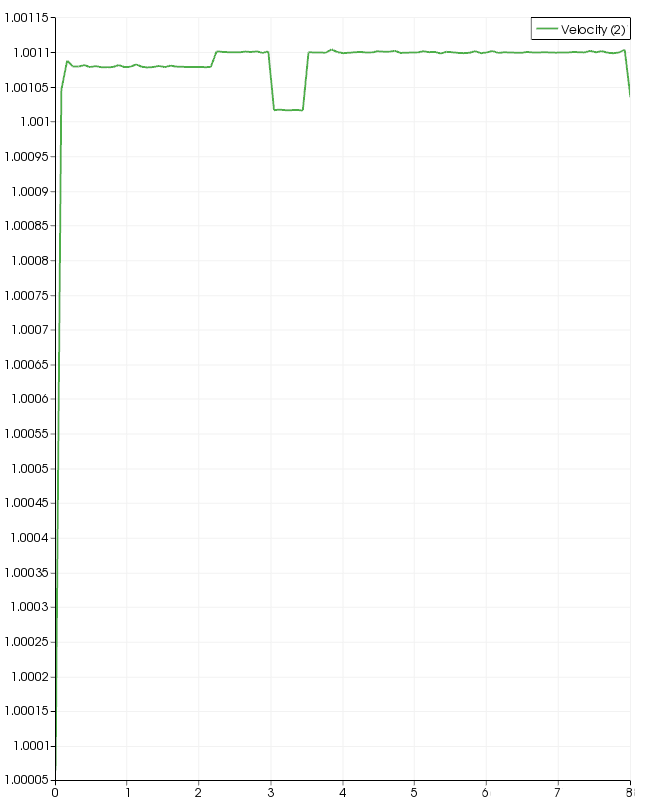
In a separate simulation the steady flow management relaxation coefficient was left at the default value of 0.1 and the pressure increase relaxation (under Global parameters) was decreased from a default of 1 to 0.1.
Revised Mesh
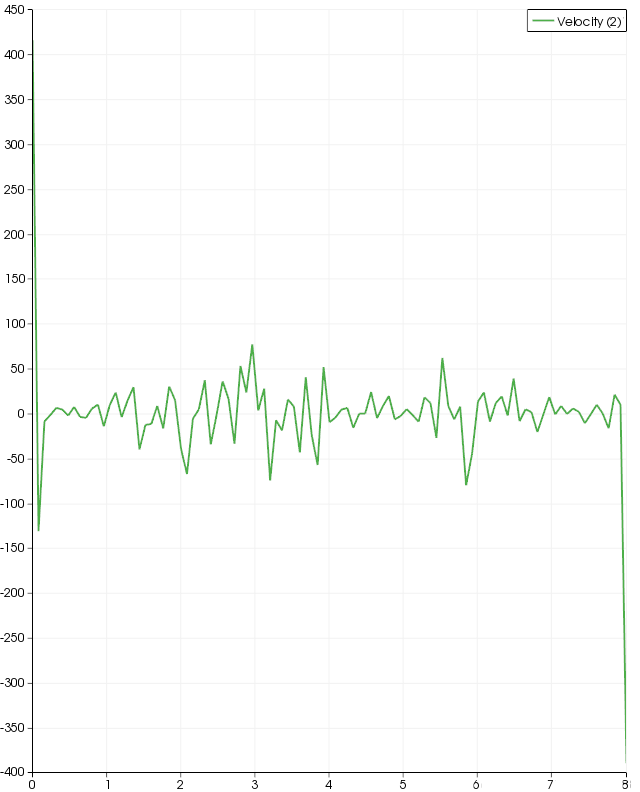
In an attempt to determine if the poor mesh quality of the previous simulations is causing the instabilities observed the number of segments of the 1/4 arc was increased to improve the elements ('slivers') at the centerline. The resulting mesh is shown below.
The resulting centerline velocity is not consistent with the Cornell Fluent tutorial results but it is a significant improvement: