Contrib:KeesWouters/solids/mooney-rivlin
- Return to: [KeesWouters]
- Return to: [solids]
Contents
Material behaviour Mooney-Rivlin
preliminary: Have to check dimensions: stresses, pressures and stiffness coefficients: [Pa] or [MPa] Following forces nearly correct ;-)
Simple block of Mooney-Rivlin material
september 2011 - Salome 6.3 - Code Aster VERSION DE DEVELOPPEMENT 11.00.10 - Ubuntu 11.04
This is a simple example of a block of Mooney-Rivlin material. As usual, the input and partly the output files can be found at the end of this contribution.
Errors are all mine.
Creative criticism welcome (of course I rather have positive than negative remarks).
Have fun.
Geometry
This is really annoying. Once again a block. The dimensions are 2Xmax*2Ymax*Lz = 5x12x43 [mm3] (Xmax = 2.5, Ymax = 6, Lz = 43 [mm]). My only excuse is that it does show the behaviour of the Mooney-Rivlin material very well.
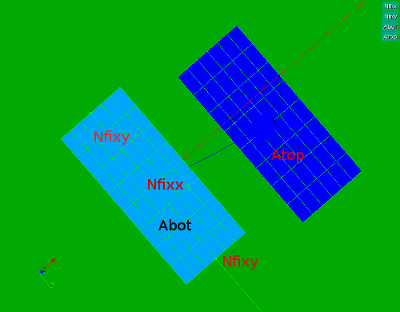
Four groups are defined on the block:
- two areas, top and bottom areas, and
- two node groups: centre node of the bottom plane and two nodes on the extreme positon of the y-axis.
The are used to define boundary conditions and pressure (load).
Loads and boundary conditions
A pressure of 6 [MPa] is applied to the top area Atop.
Note that to compare to analytic results with small strains, a pressure of 0.06 [MPa] has been used occasionally.
The boundary conditions are applied to the bottom area: all z displacements of the bottom area are restricted.
On node Nfixx the displacement in y direction is restricted.
On nodes Nfixy (two nodes on the extremes of the x axis) the displacement in x direction is restricted.
Code Aster commands
Material properties
The material propertie is given by Mooney-Rivlin.
This material behaviour is defined by a number of parameters (copied from JMB):
- C01 = 2.3456 [MPa]
- C10 = 0.709 [MPa]
- C20 = 0.0 [MPa]
- NU = 0.499 [-]
- K = 6*(C10+C01)/(3*(1-2*NU)) [MPa]
and in Code Aster called by the hyper elastic material module:
rubber=DEFI_MATERIAU(ELAS_HYPER=_F(C10=C10,
C01=C01,
C20=C20,
K=K,
RHO=1000.0),);
The parameters Cxy are coefficients of the two invariants of the Strain energy function, see eg [wiki].
For small strains the shear modulus G can be expressed as twice the sum of C01 and C10: G = 2(C01 + C10). And Youngs modulus E is equal to E = 2G(1+nu). So we have E = 4(C01+C10)(1+nu). For incompressible material the possion ratio nu --> 0.5. Hence we use nearly incompressible material here by putting nu = 0.499. Note that the numerical value of the Youngs modulus is E = 18.3 [MPa] for the values above. Later on we will use this to verify the results.
The bulk modulus K is defined in terms of Youngs modulus and poisson ratio: K = E/(3*(1-2*nu)). For nu approaching to 0.5, K approaches to infinity, ie incompressible material.
Note that nu may not be set to 0.5 exactly (to machine precision). See also paragraph 3.7 (ELAS_HYPER) of the Opérateur DEFI_MATERIAU ([u4.43.01])
Commands
FORCE=AFFE_CHAR_MECA(MODELE=Mod3d,
PRES_REP=_F(GROUP_MA='Atop',
PRES=-6.000,),);
RAMPE=DEFI_FONCTION(NOM_PARA='INST',
VALE=(0.0,0.0,
1.0,1.0,),
INFO=2);
MatRub=AFFE_MATERIAU(MAILLAGE=Mesh,
MODELE=Mod3d,
AFFE=_F(TOUT='OUI',
MATER=rubber,),);
res=STAT_NON_LINE(MODELE=Mod3d,
CHAM_MATER=MatRub,
EXCIT=(_F(CHARGE=FORCE,FONC_MULT=RAMPE,),
_F(CHARGE=DEPL,),),
NEWTON=(_F(REAC_INCR=1,
MATRICE='TANGENTE',
REAC_ITER=1,)),
COMP_INCR=_F(RELATION='ELAS_HYPER',
DEFORMATION = 'GROT_GDEP',
TOUT='OUI',),
CONVERGENCE=(_F(ARRET='OUI',
ITER_GLOB_MAXI=20)),
INCREMENT=_F(LIST_INST=LISTE,),);
Results
Displacements
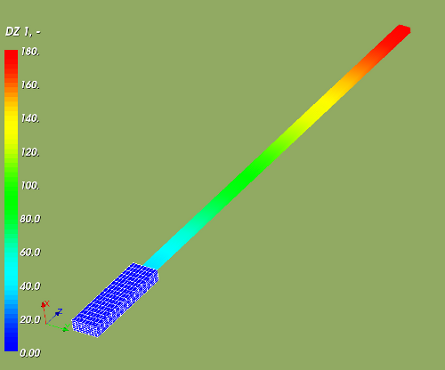
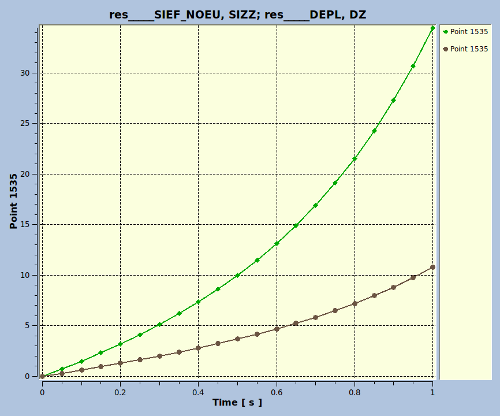
We applying a pressure load of 6 [MPa] on the top area in 20 equal steps.
The left picture below shows the overall displacements for this load. The displacements shown are real displacements (not scaled). The final z displacement is 34.441 [mm]. The strain is 34/43 ~ 0.80 [-].
In the right picture the z displacement field for a pressure of 12 [MPa] is given. The maximum displacement at the top plane is 182.5 [mm]. This is a strain of (182-43)/43 ~ 4.2 [-] (or 420 %).
We will now concentrate on the pressure case of 6 [MPa].
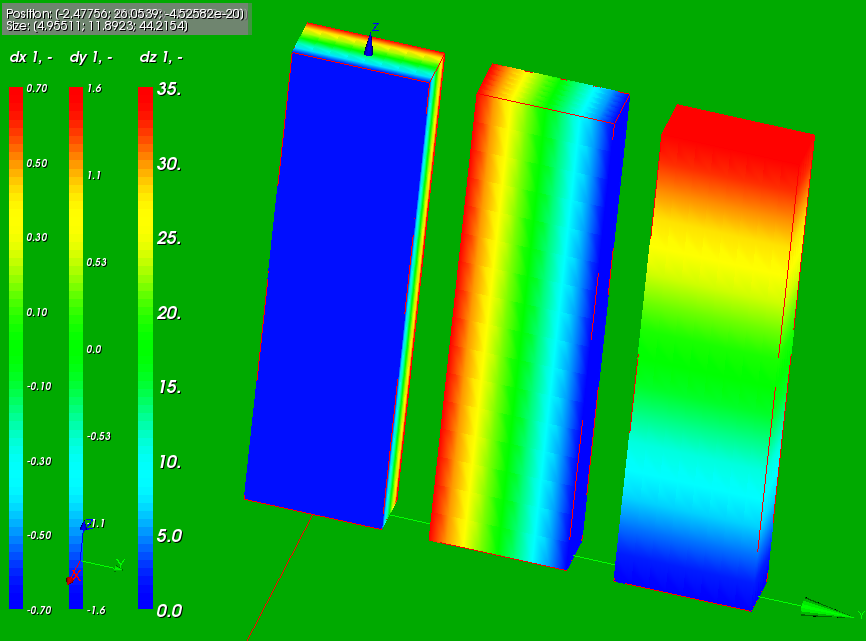
The picture below shows the displacements in x, y and z direction. The displacement in each direction are given. The maximum values are:
- dux = 0.63600 (both directions)
- duy = 1.52641 (both directions)
- duz = 43.441 (only positive direction)
Volume change
Since we put the poisson ratio nearly equal to 1/2 (nu ~ 0.5) we expect that the volume does not change. The undeformed state has a volume Vo = 2Xmax * 2Ymax * Lz = 2580 [mm3]. The deformed state has a volume of Vdef = 2(Xmax-dux)*2(Ymax-duy)*(Lz+duz) = 2583.1 [mm3], a change of 3.1 [mm3]. Taking into account the effect of the poisson ratio (nu=0.499) the volume change may be dV = Vo*eps*(1-2NU). Depending on the definition of eps this change of volume is 4.1 [mm3] (Note that maybe we have to take more digits of the displacements into account ...).
Initial stiffness
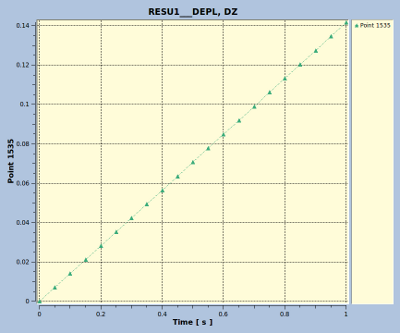
The initial stiffness of the block -ie for small axial strain- is Sz = duz/Fz = duz/PA = Lz/AE. This yields for small strains duz = P*Lz/E. For pressure P equal to 6 [Pa], the length of the block in z direction equal to 43 [mm] and the Youngs modulus E = 6(C01+C10)*(1+nu) equal to 18.3 [Pa], this yields for the initial stiffness Sz = 14.09 [N/m].
This figure shows the displacement for an end-pressure-load of 0.06 [MPa] (also calculated using 20 steps). The displacement is 0.1417 [mm]. Scaled to 6 [Pa] the displacement is 14.17 [mm]. This is slightly more than the analytic value of 14.09 [mm].
The picture has been created by right clicking in the Object Browser of the PostPro module:
- PostPro
- <result_file.med>
- fields
- Resu1_depl --> Right Click
- in the pop up window (Evolution on Point - Parameters)
- select Field
- select Point (1535 - node in top plane)
- select Component (dz)
Stress and applied pressure
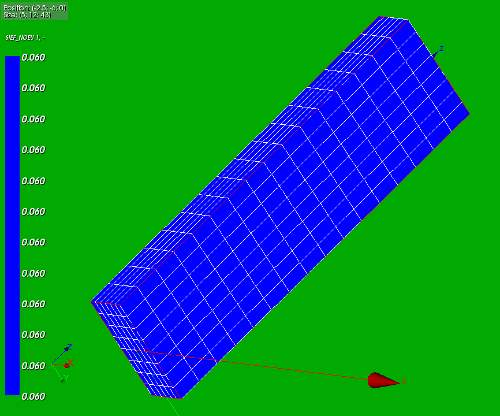
Again we have a look at the stresses (Szz) for small strains (applied pressure 0.06 [MPa]) and final stress (applied pressure 6 [MPa]. In the pictures below the stresses are shown. Not very rewarding, all blue.
The small strain stress is 0.060 [MPa] (left/top picture). This corresponds with the applied pressure and initial cross section Ainitial = 5*12 = 60 [mm2]: Szz = F/A = PA/A = P = 0.06 [MPa].
The stress at large strain is 10.793 [MPa] (right/bottom picture). Now we have to do our home work. The applied pressure is 6 [Pa]. The cross section has been reduced to Astress = 4*(Xmax-dux)*(Ymax-duy) = 33.555 [mm2]. The initial cross section is Ainitial = 60 [mm2]. So the ultimate stress will be P*Ainitial/Astress = 6*60/33.555 = 10.793 [MPa]. Nice results.
Note that this includes that the applied pressure is not scaled to the real time area. The applied pressure is being translated to node forces initially and remain the same during the calculation.
In fact we applied a constant pressure on the top plane that is not being update or followed during the calculations. The default command, from the *.mess file is:
res=STAT_NON_LINE(EXCIT=
_F(TYPE_CHARGE='FIXE_CSTE',CHARGE=FORCE,FONC_MULT=RAMPE),
_F(TYPE_CHARGE='FIXE_CSTE',CHARGE=DEPL)),
....);
where TYPE_CHARGE='FIXE_CSTE', or fixed during the calculations.
Stress and applied pressure II - Following force
In the output of the mess file we see that the default TYPE_CHARGE is 'FIXE_CSTE':
res=STAT_NON_LINE(EXCIT=(_F(TYPE_CHARGE='FIXE_CSTE',
CHARGE=FORCE,
FONC_MULT=RAMPE),
_F(TYPE_CHARGE='FIXE_CSTE',
CHARGE=DEPL)),
....);
This means that the pressure distribution is not updated, and we add the in the STAT_NON_LINE command the key word TYPE_CHARGE='SUIV'. The pressure will be updated according to the geometry during the steps:
pressure = -6.000
FORCE=AFFE_CHAR_MECA(MODELE=Mod3d,
PRES_REP=_F(GROUP_MA='Atop',
PRES=pressure),);
res = STAT_NON_LINE(...
EXCIT=(_F(CHARGE=FORCE,FONC_MULT=RAMPE,TYPE_CHARGE='SUIV'),...)
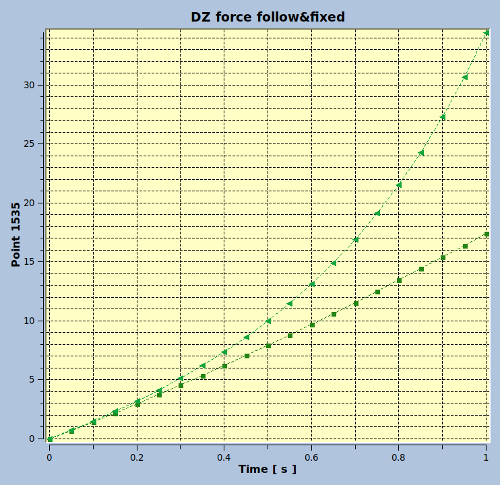
The key word TYPE_CHARGE='SUIV' states that the pressure distribution will follow the momentary geometry of its surface during each step in the calculation. In the picture below the displacement Uz is shown for each step, both for fixed and following force/pressure. The fixed pressure is the same as before, where the stiffness decreases with increasing pressure. The final displacement is 34 [mm]. The following pressure shows a straight line, indicating that the reduced stiffness is compensated by an smaller area of the top plane where the pressure is being applied. At step 20 (time 1) the displacement of the topplane is ~17.3 [mm].
Some characteristics for the final situation, P = 6.0 [MPa]:
Displacements:
the maximum x and y displacments of the block are Ux = 0.390378 [mm] and Uy = 0.936908 [m]
the z displacement of the top plane is Uz = 17.426 [mm]
Stresses:
The stresses Sxx and Syy are: Sxx = Syy = 0.0 [MPa]
the stress Szz is equal to 6.0 [MPa]: this is exactly the stress defined by the following pressure!
Strains:
The strains EPxx and EPyy are: EPxx = EPyy = -0.156151
The strain EPzz is: EPzz = 0.405255
From the displacements we derive:
|EPxx| = 0.390378/2.5 = 0.156151
|EPyy| = 0.936908/2.5 = 0.156151
EPzz = 17.426/ = 0.405255, in accordance with the values above.
Still need to check the following:
For uniaxial loading the Green strain tensor F is defined by:
| 1+EPxx 0.0000 0.0000 | | 0.84390 0.00000 0.00000 |
F = | 0.0000 1+EPxx 0.0000 | = | 0.00000 0.84390 0.00000 |
| 0.0000 0.0000 1+EPzz | | 0.00000 0.00000 1.40526 |
| 1.97474 0.00000 0.00000 |
C = FtF = | 0.00000 0.71208 0.00000 |
| 0.00000 0.00000 0.71208 |
then
Ic1 = 3.3989 --> Ic1-3 = 0.3989 Ic2 = 3.3194 --> Ic2-3 = 0.3194 Ic3 = 1.0013 --> Ic3 ~ 1.0
For incompressible material, the third invariant of the strain tensor C = FtF is 1. So the value Ic3 is in good agreement with this.
finally the stress Szz is given by:
Szz = 2*(C01/EPzz+C10)*(EPzz^2-1/EPzz) = 6.0078 [MPa]
So why is the relation between the steps and z displacement linear now?
Input files - download
Input files:
- Python script for defining the geometry and mesh. Load this file in Salome by File --> load script (cntrl T in the object browser), refresh (F5) after running.
- Save the mesh by:
- change to Mesh module
- right clicking in the object browser by right clicking on the mesh name Mblock; select Export to MED
- change mesh file name to Mblock.med (no need) and click save
- Save the mesh by:
- ASTK files (you need to edit the path to your requirements ...). To start Code Aster calculation press Run. Interactive enabled, Interactive-follow-up disabled, nodebug enabled.
- command file. Same remark as ASTK file.
Have fun.
Comments welcome.
Tested with CA version 11.00.31 (needed, for following force SUIV, lower version contain bug on this) and Salome 6.3.1.
groeten - Kees