Difference between revisions of "Contrib:KeesWouters/Homard/lshape"
m (Reverted edit of Atywehacyg, changed back to last version by Claws) |
|||
| Line 1: | Line 1: | ||
| − | + | =='''Mesh refinement by the macro command MACR_ADAP_MAIL'''== | |
['''under construction - just started 2010-02-21 ... '''] | ['''under construction - just started 2010-02-21 ... '''] | ||
Latest revision as of 13:02, 18 November 2010
Contents
Mesh refinement by the macro command MACR_ADAP_MAIL
[under construction - just started 2010-02-21 ... ]
To start with, this contribution mainly focuses on the use of Salome, Code Aster and the macro command MACR_ADAP_MAIL. So I do not focus on the results and the mechanical justifications of the code that has been used. So no guarantee that the results will be correct up to five decimal places, which they are probably not. I do hope though that this information is useful. For me it has been, because I had to think about some commands and look through the documentation and learn from that. In case of mistakes, errors or remarks, please notify me, or better, you are invited to correct or edit them yourself. Enjoy.
The geometry
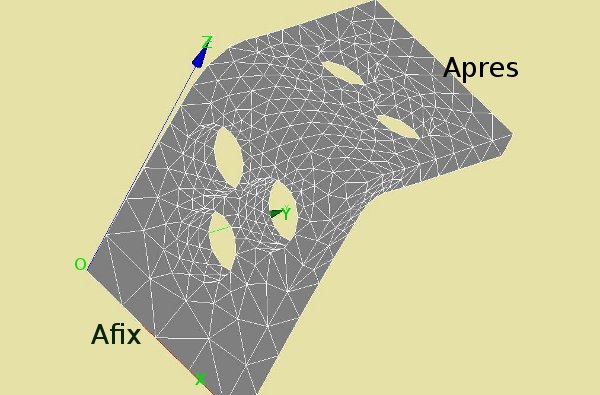
The geometry and the mesh of the construction
The mesh refinement is based on Homard. As usual the geometry is quite simple in order not to disturb the issue we would like to show with other difficulties. We try to refine the mesh of an L shape with a few holes in it. The thickness of the two 'legs' are 0.8 mm and 1.2 mm. The diameters of the holes vary between 0.9 and 1.0 mm. Outline dimensions of the shape are [Width * Depth * Height] = [5 * 6 * 7] mm3.
The geometry is defined in a python script (for download see end of this contribution) and can be loaded into Salome Geometry module by File --> Load script (or ctrl T in the object browser window). Right click Refresh or push F5 after loading if necessary.
- overall dimension: [x,y,z] = [5.0, 6.0, 7.0] mm
- width of the legs: 1.2 mm vertical and 0.8 mm horizontal
- diameters of the circles: in vertical plate: 0.9 mm - in horizontal plate: 0.8 mm
- radii of the fillets: innerfillet 0.5 mm - outerfillet 1.2 mm
The mesh consists of coarse, tetrehedral elements to start with.
The load of the construction
The L shape is fixed in all directions at the bottom area Afix. The area at opposite end of L is denoted Apres. For simplicity, on this area a displacement of 0.1 mm is given in the y direction.
The general idea of the refinement
The general idea of the Homard refinement is to start with a rather course mesh and update the mesh according to a criterium. In this case we use the stress error estimate ERRE_ELEM_SIGM and its component ERREST. For more details on this error estimation see U7.03.01.pdf. To start with, a standard load case will be performed and an error estimation on all the elements will be carried out. Depending on a criterium defined in the macro command the mesh will be adapted. In this example a certain percentage of the elements with the highest error estimates will be refined. A new calculation with the adapted mesh can take place. For this calculation all the models, loads and parameters need to be rebuild. So it is most suitable to define geometrical entities (GROUP_MA) in the mesh in stead of nodes.
To summarise:
- initial some parameters
- read initial mesh
- define material properties
- define number of refinement iterations (whether or not fixed)
- loop through:
- ...define model
- ...apply material to model
- ...apply load to model
- ...perform calculation
- ...determine element and node parameters
- ...(write output data)
- ...refinement of mesh MACR_ADAP_MAIL
The error estimation is determined in the CALC_ELEM command, by the option 'ERRE_ELEM_SIGM':
result...=CALC_ELEM(....,OPTION=(....,'ERRE_ELEM_SIGM',),);
The refinement command itself is as follows:
......
refmesh = CO('refmesh')
MACR_ADAP_MAIL(MAILLAGE_N=curmesh,
MAILLAGE_NP1=refmesh,
ADAPTATION='RAFFINEMENT',
RESULTAT_N=result...,
INDICATEUR='ERRE_ELEM_SIGM',
NOM_CMP_INDICA='ERREST',
CRIT_RAFF_PE=0.30,
QUALITE='OUI',
CONNEXITE='OUI',
TAILLE='OUI',);
The command takes the current mesh curmesh as input MAILLAGE_N=curmesh and the output mesh is MAILLAGE_NP1=refmesh. Since the parameter refmesh is not yet defined (in the Python sense), we need to apply the operator CO('refmesh') to define it. [If an unknown parameter is needed in the right hand side of a command, we always need to apply this operator.] Further keywords are the ADAPTATION='RAFFINEMENT' together with CRIT_RAFF_PE=0.30. In this case 0.30 or 30 % of the elements with the largest error estimate (based on stress error indicator INDICATEUR='ERRE_ELEM_SIGM', NOM_CMP_INDICA='ERREST') are refined. The other elements remain untouched. Note that 30 % refinement of volume elements yields a significant amount of new elements. See table at the result part.
The detailed command of the refinement
In this case we perform two refinements of the mesh, ie. three standard calculations are performed. Each refinement of the mesh is based on a parameter of the previous calculation.
The standard calculation
This set of commands is a standard calculation. The only command that should be added for a complete calculation is FIN():
DEBUT();
#Read MED mesh file mesh0=LIRE_MAILLAGE(UNITE=20,FORMAT='MED',NOM_MED='mesh0',INFO_MED=2,INFO=1,);
#Assign to the Model
model0=AFFE_MODELE(MAILLAGE=mesh0,AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',MODELISATION='3D',),);
#Define material properties steel=DEFI_MATERIAU(ELAS=_F(E=2.1e5,NU=.28,),);
#Assign material to mesh Amat0=AFFE_MATERIAU(MAILLAGE=mesh0,AFFE=_F(TOUT='OUI',MATER=steel,),);
# define boundary conditions and loads
Load0=AFFE_CHAR_MECA(MODELE=model0,
DDL_IMPO=(_F(GROUP_MA='Afix',DX=0.0,DY=0.0,DZ=0.0,),
_F(GROUP_MA='Apres',DX=0.0,DY=0.1,DZ=0.0,),),);
result0=MECA_STATIQUE(MODELE=model0,CHAM_MATER=Amat0,
EXCIT=_F(CHARGE=Load0,),),);
result0=CALC_ELEM(reuse =result0,MODELE=model0,RESULTAT=result0,
TOUT='OUI',TYPE_OPTION='TOUTES',
OPTION=('EQUI_ELNO_SIGM','SIEF_ELNO_ELGA','ERRE_ELEM_SIGM',),);
result0=CALC_NO(reuse =result0,RESULTAT=result0,OPTION=('EQUI_NOEU_SIGM',),);
IMPR_RESU(FORMAT='MED',UNITE=80,RESU=_F(MAILLAGE=mesh0,RESULTAT=result0,
NOM_CHAM=('EQUI_ELNO_SIGM','EQUI_NOEU_SIGM','ERRE_ELEM_SIGM','DEPL',),),);
The first refinement - on mesh0
The mesh0 is refined. The refined mesh is available under the name mesh1. Now exactly the same, standard calculation is being performed. The models, loads and material properties first need to be based on mesh1. So also the assingments for this new mesh need to be carried out. The results are now written to unit 81 in stead of unit 80.
MACR_ADAP_MAIL(MAILLAGE_N=mesh0,
MAILLAGE_NP1=CO('mesh1'),
ADAPTATION='RAFFINEMENT',
RESULTAT_N=result0,
INDICATEUR='ERRE_ELEM_SIGM',
NOM_CMP_INDICA='ERREST',
CRIT_RAFF_PE=0.30,
QUALITE='OUI',
CONNEXITE='OUI',
TAILLE='OUI',);
model1=AFFE_MODELE(MAILLAGE=mesh1,AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',MODELISATION='3D',),);
Load1=AFFE_CHAR_MECA(MODELE=model1,
DDL_IMPO=(_F(GROUP_MA='Afix',DX=0.0,DY=0.0,DZ=0.0,),
_F(GROUP_MA='Apres',DX=0.0,DY=0.1,DZ=0.0,),),);
#Assign material to mesh Amat1=AFFE_MATERIAU(MAILLAGE=mesh1,AFFE=_F(TOUT='OUI',MATER=steel,),);
result1=MECA_STATIQUE(MODELE=model1,CHAM_MATER=Amat1,
EXCIT=(_F(CHARGE=Load1,),),);
result1=CALC_ELEM(reuse =result1,MODELE=model1,RESULTAT=result1,
TOUT='OUI',TYPE_OPTION='TOUTES',
OPTION=('EQUI_ELNO_SIGM','SIEF_ELNO_ELGA','ERRE_ELEM_SIGM',),);
result1=CALC_NO(reuse =result1,RESULTAT=result1,OPTION=('EQUI_NOEU_SIGM',),);
IMPR_RESU(FORMAT='MED',UNITE=81,
RESU=_F(MAILLAGE=mesh1,RESULTAT=result1,
NOM_CHAM=('EQUI_ELNO_SIGM','SIGM_NOEU_DEPL','DEPL','SIEF_ELNO_ELGA','ERRE_ELEM_SIGM',),),);
The second refinement - on mesh1
Same procedure as before but now carried out on mesh1 and the output is the refined mesh2. Of course, the models, loads and material properties need to be based on mesh2 now. The results are now written to unit 82.
MACR_ADAP_MAIL(MAILLAGE_N=mesh1,
MAILLAGE_NP1=CO('mesh2'),
ADAPTATION='RAFFINEMENT',
RESULTAT_N=result1,
INDICATEUR='ERRE_ELEM_SIGM',
NOM_CMP_INDICA='ERREST',
CRIT_RAFF_PE=0.30,
QUALITE='OUI',
CONNEXITE='OUI',
TAILLE='OUI',);
model2=AFFE_MODELE(MAILLAGE=mesh2,AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',MODELISATION='3D',),);
Load2=AFFE_CHAR_MECA(MODELE=model2,
DDL_IMPO=(_F(GROUP_MA='Afix',DX=0.0,DY=0.0,DZ=0.0,),
_F(GROUP_MA='Apres',DX=0.0,DY=0.1,DZ=0.0,),),);
#Assign material to mesh Amat2=AFFE_MATERIAU(MAILLAGE=mesh2,AFFE=_F(TOUT='OUI',MATER=steel,),);
result2=MECA_STATIQUE(MODELE=model2,CHAM_MATER=Amat2,
EXCIT=(_F(CHARGE=Load2,),),);
result2=CALC_ELEM(reuse =result2,MODELE=model2,RESULTAT=result2,
TOUT='OUI',TYPE_OPTION='TOUTES',
OPTION=('EQUI_ELNO_SIGM','SIEF_ELNO_ELGA','ERRE_ELEM_SIGM',),);
result2=CALC_NO(reuse =result2,RESULTAT=result2,OPTION=('EQUI_NOEU_SIGM',),);
IMPR_RESU(FORMAT='MED',UNITE=82,
RESU=_F(MAILLAGE=mesh2,RESULTAT=result2,
NOM_CHAM=('EQUI_ELNO_SIGM','SIGM_NOEU_DEPL','DEPL','SIEF_ELNO_ELGA','ERRE_ELEM_SIGM',),),);
FIN(FORMAT_HDF='OUI',);
The results of the refinement
The numbers of nodes and quadratic elements (tetrahedrons) of the meshes:
30% 70% 30%-->new factor nodes elements changed unchanged elements change 4224 2064 620 1444 16346 9636 2890 6746 8192 13 (=8192 / 620) 65845 42537 12760 29777 35791 12 (=35791/2890)
So, from a single tetrahedron that is refined, 12 to 13 tetrahedrons are generated for this mesh.
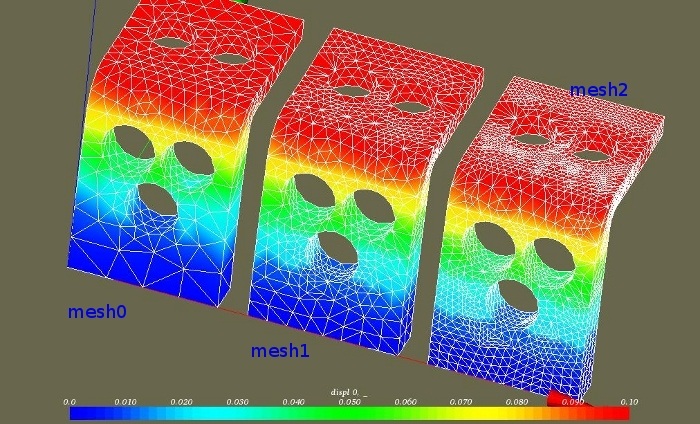
In the graph below, the original mesh (top left) and the two successive refinements based on the discussed criteria are depicted (bottom right last iteration).
The picture below shows the stress error estimation 'ERREST'. The first refinement is based on this field: mesh0 --> mesh1.
The error estimation field 'ERROR-ELEM_SIGMA' containes 10 components:
ERREST, NUEST, SIGCAL, TERMRE,TERMR2,TERMRENO,TERMN2,TERMSA,TERMS2, TAILLE.
Any of these components can be used in the component indicator, eg. NOM_CMP_INDICA='ERREST'
General remarks
In the CA forum, Delmas wrote:
... In Code_Aster, the field "ERREUR" has many components. But you have to consider only the two first (ERREST and NUEST). ERREST is an absolut value and NUEST is relative value (absolute value normalised with the stress tensor norm).
Also from the CA forum:
In order to avoid a too fine mesh, you can use the keyword NIVE_MAX in the macro MACR_ADAP_MAIL. Eg. if NIVE_MAX = 5, the mesh will not be more than 5 times finer than the initial mesh.
You can also use the unrefinement (RAFF_DERAFF) command on elements far away from the critical zone.
The ASTK input files
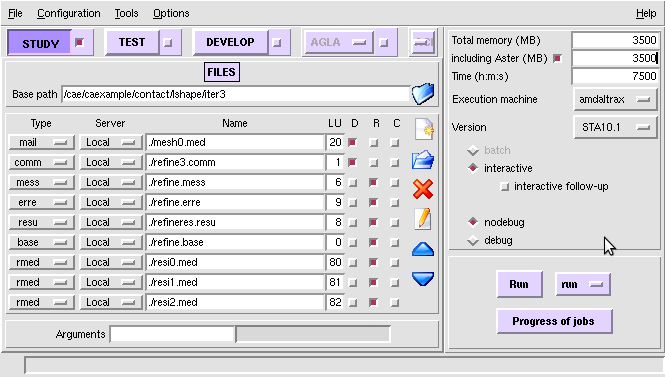
The picture below shows the input and output files defined in ASTK.
Download files
This zip contains the following files
- python geometry and mesh files (load in Salome by File --> Load script (cntrl T)) and right select refresh (F5) in the object browser). Export the med file in the mesh module under mesh0.med for further processing by Code-Aster, controlled by ASTK.
- command files for Code-Aster
- astk file for file control by ASTK
- export file, generated by ASTK.
The result files resi0.med, resi1.med and resi2.med, can be viewed in the post processor module of Salome by File --> Import --> resix.med or cntrl I in the object browser.
Links
More information about the mesh refinement by Homard can be find here:
pdf file: http://www.code-aster.org/V2/doc/default/man_u/u7/u7.03.01.pdf
Homard website: http://www.code-aster.org/outils/homard
That's it for now.
Kees